また,そのとき使った合同条件をかきなさい。 3右の図の四角形ABCDで, AB=CB,AD=CDです。 この図で,合同な三角形の組を,記号≡を使って 表しなさい。 また,そのとき使った合同条件をかきなさい。 45° ウ エ 55° 65° イ 55° ア 65° キ 45° オ 55° 65°特殊な四角形の定義 正方形: すべての角が直角ですべての辺の長さが等しい四角形 長方形: すべての角が直角な四角形 ひし形: すべての辺の長さが等しい四角形 平行四辺形: 向かい合う2組の辺が平行な四角形 台形: 向かい合う1組の辺が平行な四角形 注意点として、 "長方形" や "ひし形" も向かい合う辺は平行なので 『平行四辺形の定義』 に3点目は、合同な三角形で明らかにしたこと、つ まり「合同の3条件」が四角形の場合も適用できる かと類推したり、一般化について確かめようとしたり する姿勢である。本時では2点目と3点目を重視し た指導を試みる。 関心 意欲 態度
Http Www Fdtext Com Dan Fdn S2 05 Goudou Pdf
四角形の合同条件 証明
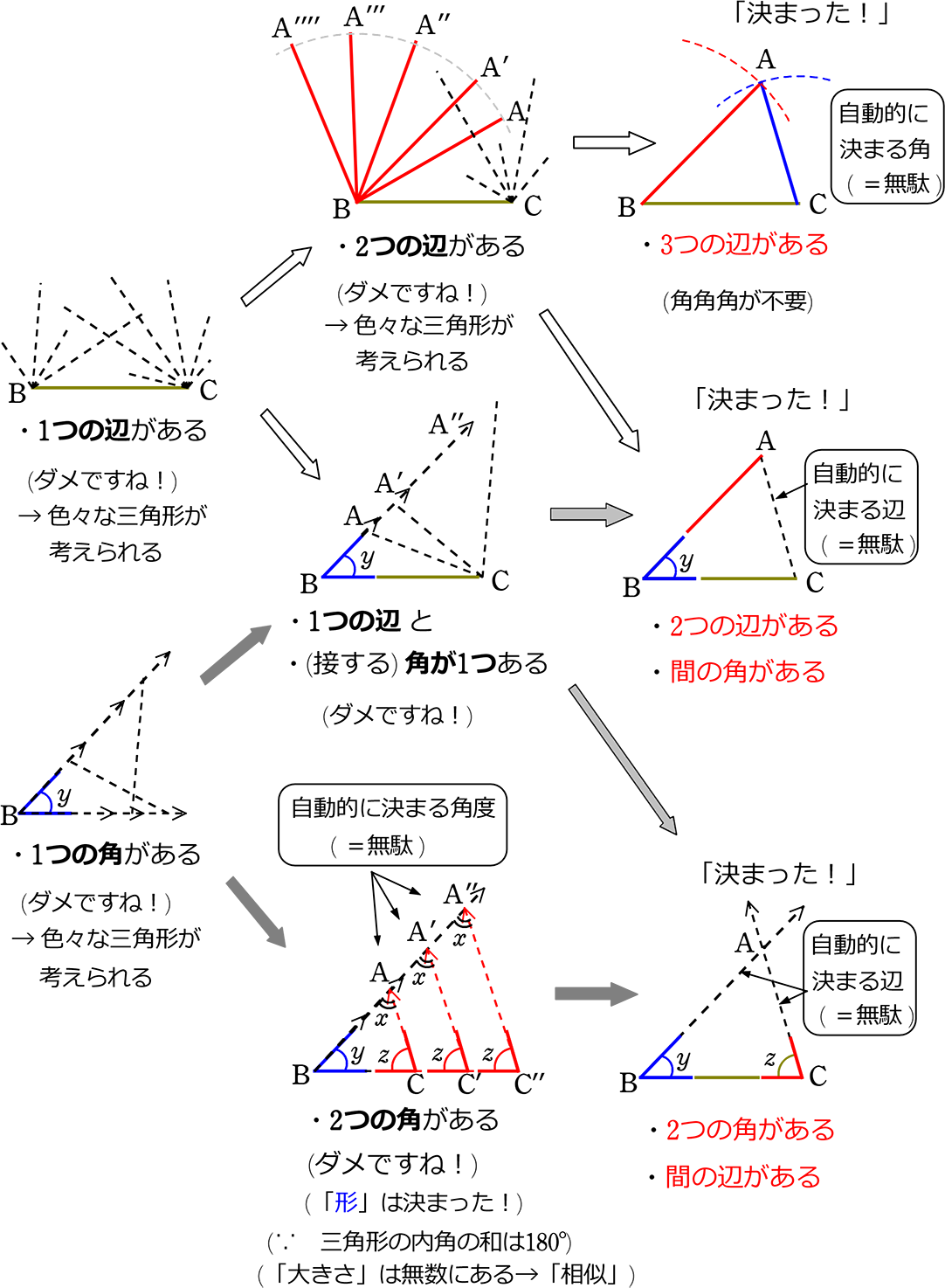
四角形の合同条件 証明- 相似条件と合同条件の違いとは? Tooda Yuuto 18年7月24日 2つの三角形が合同であることを示すための条件を、 三角形の合同条件 と言います。 以下の3つの合同条件のうち、 どれか1つでも成り立っている なら「それらの三角形は合同である」ということが 算数では、三角形の合同条件に深くは触れません。 しかし実際には、三角形の作図の際、合同条件は無意識ながらも暗に用いています。 そこで、その合同条件を明確に発見する授業を試みました。 なぜなら、合同条件を子どもが見いだす際に「反例をあげる」という重要な思考方法を経験させることができるからです。 合同な三角形を作図するために必要な情報



平面図形の基礎
3 単 元 ¡ 「三角形・四角形」 4 単元について (1) 単元観 本単元は,数学科学習指導要領〔第2学年〕「B 図形」の領域に示されている,(2)ウ「三角 形の合条件などを基にして三角形や平行四辺形の基本的な性質を論理的に確かめたり,図形の性仮定と結論,逆,合同条件 問題 次の①~④のことがらの中から逆が正しいものをすべて選び,番号を書け。 ① b整数 a, で,aもb も偶数ならば,abは偶数である。 ② ABC で,AB=AC ならば,∠B=∠C である。 ③ 2 つの直線 まとめ:ひし形は平行四辺形の1種!! 4つの辺がすべて等しい四角形 がひし形の定義だったね。 この定義から、 2組の辺がそれぞれ等しい っていう平行四辺形になる条件が使えて、 ひし形は平行四辺形であることがいえるんだ。 テスト前にしっかり復習
三角形の合同条件や平行四辺形になるための 条件を用いて,AE=CFとなることを証明 してみましょう。 桃子さんの証明を振り返ってみましょう。 桃子さんは何に着目して証明していますか。 この証明で用いられている三角形の合同条件と形の合同条件が根拠として必要である.既知 である一般の三角形の合同条件の限界を感じ させ,新たな知識の必要性につなげたい. 導入問題 右の図で 長さが等しい線分は あるでしょうか. いろいろな三角形や四角形では どんな性質が成り立つのか?1 単元名 「5章 三角形と四角形」 2 留萌管内の全国学力・学習状況調査から見える実態(h24年度北海道教育委員会hp結果から) 留萌管内と全道の比較をしたところ,数 学a 全体では-45,図形領域においては -43 と全道よりやや低いという結果であ
四角形abcdの内角の和は360°なので、 ∠b=360° (80°65°85°)=130° ・・・(答え) 三角形の合同 次は、三角形に焦点を当てて合同条件を見ていこう! 三角形の合同条件3つ まずはイメージしてみよう!合同条件は、この3つだ。 三角形の合同条件①長方形、ひし形、正方形の定義 ☆平行四辺形に条件を付け加えると、どんな四角形になるかを見いだす。 長方形、ひし形、正方形と平行四辺形の関係 小学生・中学生が勉強するならスクールtv。全国の学校の教科書に対応した動画で学習できます。三角形の合同条件 3組の辺がそれぞれ等しい。 2組の辺とその間の角がそれぞれ等しい。 1組の辺とその両端の角がそれぞれ等しい。




急ぎです 全て埋めていただきたいです 図形と合同 平行四辺形になる条件 Clear



1
三角形の合同条件は、・3辺がそれぞれ等しい。 ・2辺とその間の角がそれぞれ等しい。 ・1辺とその両端の角がそれぞれ等しい。 ですが、四角形の合同条件、四面体の合同条件というものは聞いたことがありません。どのようなものか教三角形 四角形 三角形の内角の和 𝟖 ° 平行四辺形 定義2組の対辺がそれぞれ平行な四角形 三角形の外角は、それととなり合わない 2つの内角の和に等しい 2組の 対辺はそれぞれ等しい 三角形の合同条件① 3組の辺がそれぞれ等しい三角形の合同条件のようであるが、これらは、三角形 がただ1つに決まるための三角形の決定条件である。 合同条件は、2つの三角形が合同かどうかを判断する ための条件であり、2つの図形の比較を行っている点 で、小学校での扱われ方の違いが見られる。
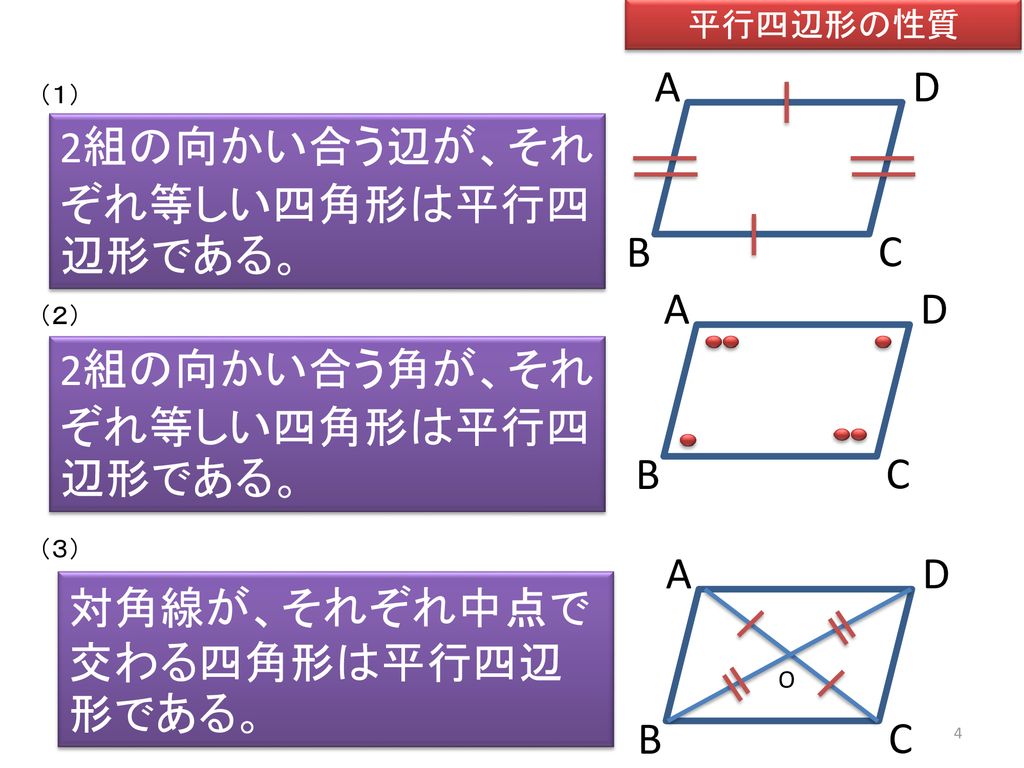



平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download
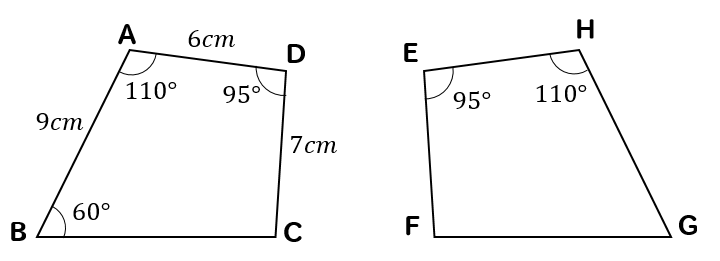



中学数学 合同な図形の性質とは 見つけ方は 問題を使って解説 数スタ
二等辺三角形の性質/二等辺三角形になることを証明:角/三角形の合同利用/ 二等辺三角形の計算問題 /正三角形などの証明問題/正三角形などの計算問題/ 直角三角形の合同条件/ 直角三角形と二等辺三角形/垂線をひく/2 つの内角の和=90°本文抜粋 1 はじめに 「先生,三角形の合同条件には,三辺相等・二辺挟角相等・二角挾辺相等の三つがあることはわかりました。 それでは,四角形の合同条件はどうなっているのですか 対象1 50 1 31 55 15 15 11 12 184 184 11, 12 O, 1 50 1 1 7—, 600 10 900 900 P 185 184 184 p 185
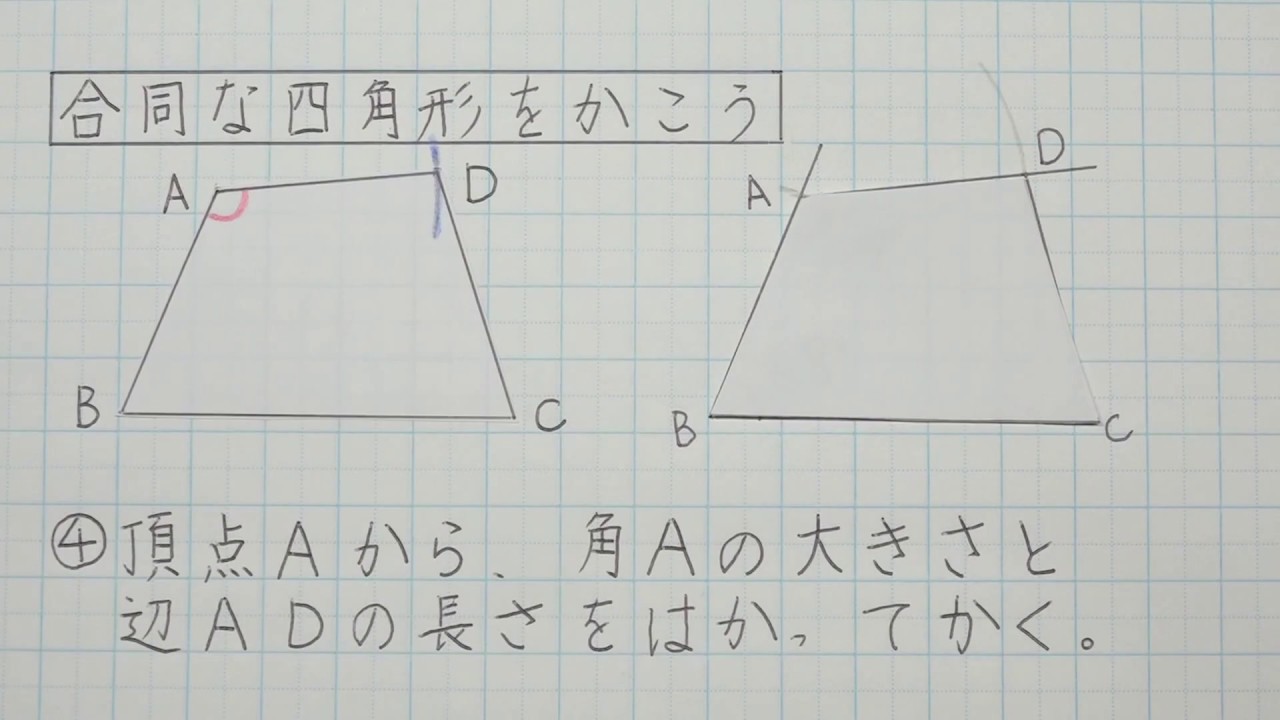



5年算数 図形の角と合同 5 合同な四角形をかこう Youtube




中学2年生の数学 証明 三角形の合同条件と証明の書き方 塾講師が数学をやりmath
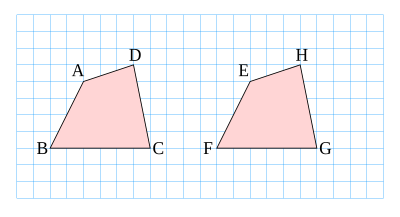
合同と三角形,四角形 1③ ₁ 右の2 つの四角形は 合同です。 (60 点) ① 次の頂 ちょう 点 てん と対 たいおう 応する頂点を書きましょう。 頂点aと 頂点bと 頂点cと 頂点dと ② 次の辺と対応する辺を書きましょう。 辺abと 辺bcと 辺cdと 辺daと直角三角形で、直角に対する線を 斜辺 (しゃへん) という。 直角三角形の場合、三角形の合同条件に加え、次の条件がある。 たったこれだけの情報だけでも、直角三角形が合同だといえる。 「斜辺とそれ以外の辺がそれぞれ等しい」については、中学3合同条件を使って 合同な三角形を見 分け、合同であるこ とを記号を使って 表すことができる。 図形の基本性質や 三角形の合同条件、 証明の必要性と意 味及び証明のしく みなどについて理 解している。 7 指導計画 節 小節 時 学習内容 用語・記号
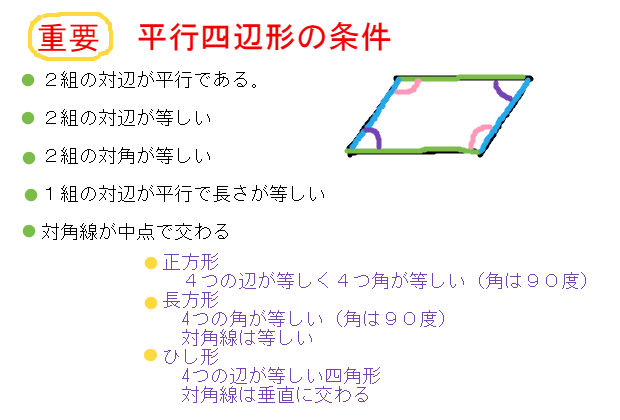



三角形の合同の応用問題 制限3分 中学数学 理科 寺子屋塾の復習サイト




正方形 Wikipedia
合同条件と相似条件をそれぞれ見ていこっか。 合同条件1「3つの辺の長さがそれぞれ等しい」 「3つの辺の長さ」 がすべて等しいっていう条件は合同条件だ。 この条件を満たす三角形たちは合同である、ってことが言えるわけね。 四角形の合同条件について教えて下さい 平行四辺形abcdの辺ad,bcの中点をそれぞれe,fとする af=beがなりたつとき、abcdは長方形であることを証明しなさい という問題の場合の過程で 四角形afcdと四角形bedcについて af=be fc=ed cd=dc da=cb よって 四角形afcd≡四角形bedc と言え直角三角形の合同条件 直角三角形の合同条件 2つの直角三角形は、次の場合に合同である。 1 斜辺と1つの鋭角が、それぞれ等しいとき(証明) 2 斜辺と他の1辺が、それぞれ等しいとき(証明)




5年算数 図形の角と合同 7 いろいろな方法で合同な四角形をかこう あなたの人生はあなたの思い描いたとおりになる




5章 三角形と四角形 タカラゼミ
平行線の性質,三角形の角についての性質,三角形の合同条件,図形の証明の必要性と意味及び その方法などを理解することができる。 (数量や図形などについての知識・理解) 3指導に当たって 第1学年では,図形の作図や移動を取り扱っている。平行四辺形の性質や三角形の合同条件、平行線の性質の復習を行う。 本時の学習内容「四角形がどのような条件をもてば、平行四辺形になるか考えよう」を知る。 教科書124ページの「ひろげよう」に しかし、対角線を考慮に入れなければ、四角形の合同条件は次のようになりそうだ。 (1)4辺と1角 (2)3辺と2角(3辺の2夾角) (3)2辺と3角 そして、これをN角形の合同条件に一般化すれば、 (1)n辺と (n-3)角



合同 時事用語事典 情報 知識 オピニオン Imidas イミダス



4つの辺が等しくても 合同ではない四角形を描くにはどのようにしたらよいのでし Yahoo 知恵袋
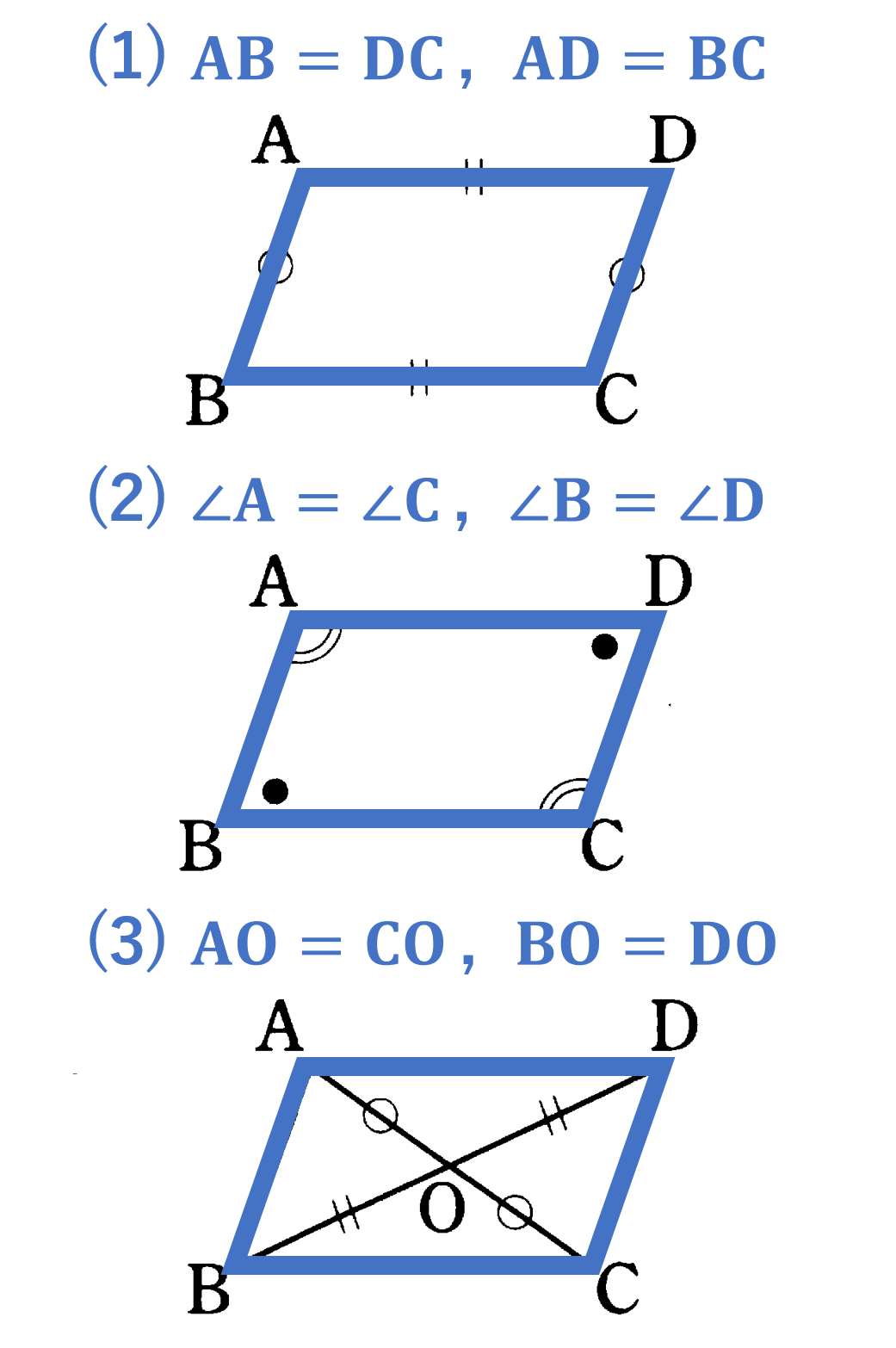
平行四辺形になる条件 四角形は、次の性質のどれかをもつと、平行四辺形である。 1 2組の向かいあう辺が、それぞれ平行である。(定義) 2 2組の向かいあう辺が、それぞれ等しい。(証明) 3 2組の向かいあう角が、それぞれ等しい。(証明)
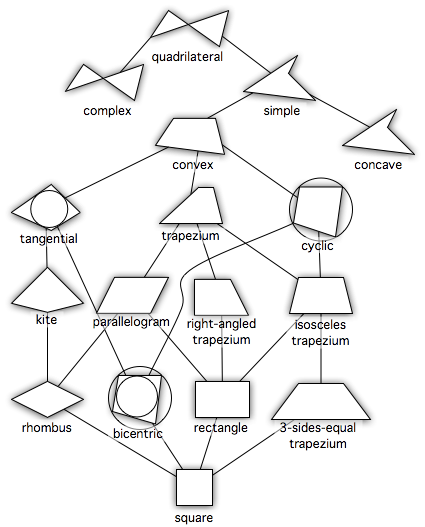



四角形 Wikipedia



四角形 Wikipedia




5年算数 図形の角と合同 3 四角形を対角線で分けて 合同な三角形をつくろう Youtube



Www Mext Go Jp Component A Menu Education Detail Icsfiles Afieldfile 0427 Mxt Kouhou02 084 Pdf




三角形と四角形 三角形の合同の証明のしかた 中学数学 定期テスト対策サイト



平面図形の基礎
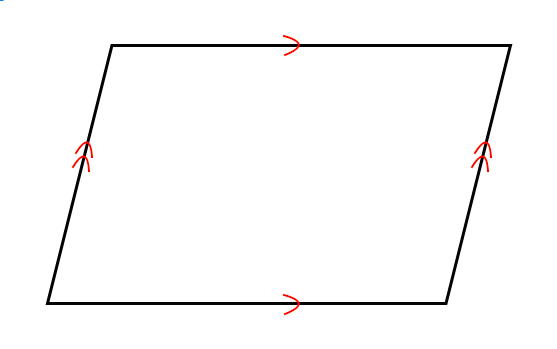



合同な三角形 平行四辺形で証明 苦手な数学を簡単に
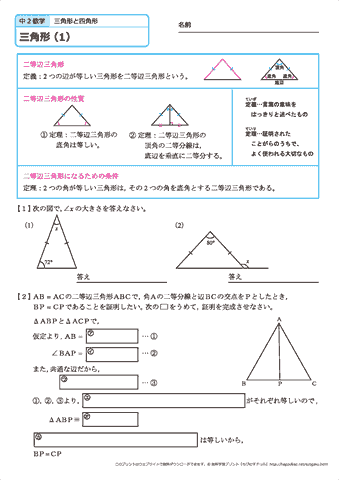



中学2年生 数学 三角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Http Www Impuls Tgu Org Cms Templates File Php Url 2fcms 2flibrary Pdf Files 2f122 2fsugekari15jp Pdf



2
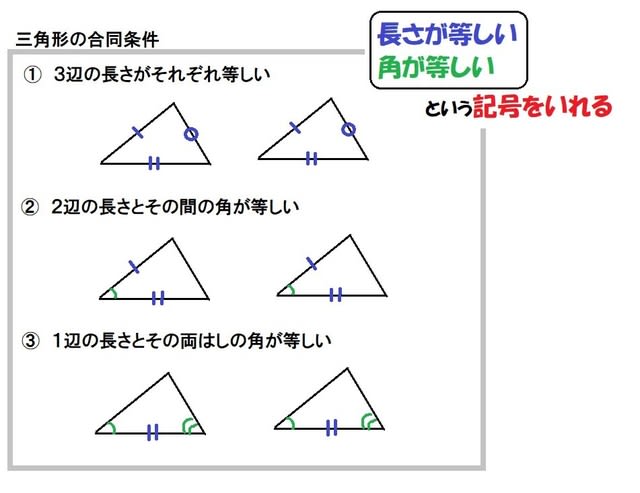



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学



1
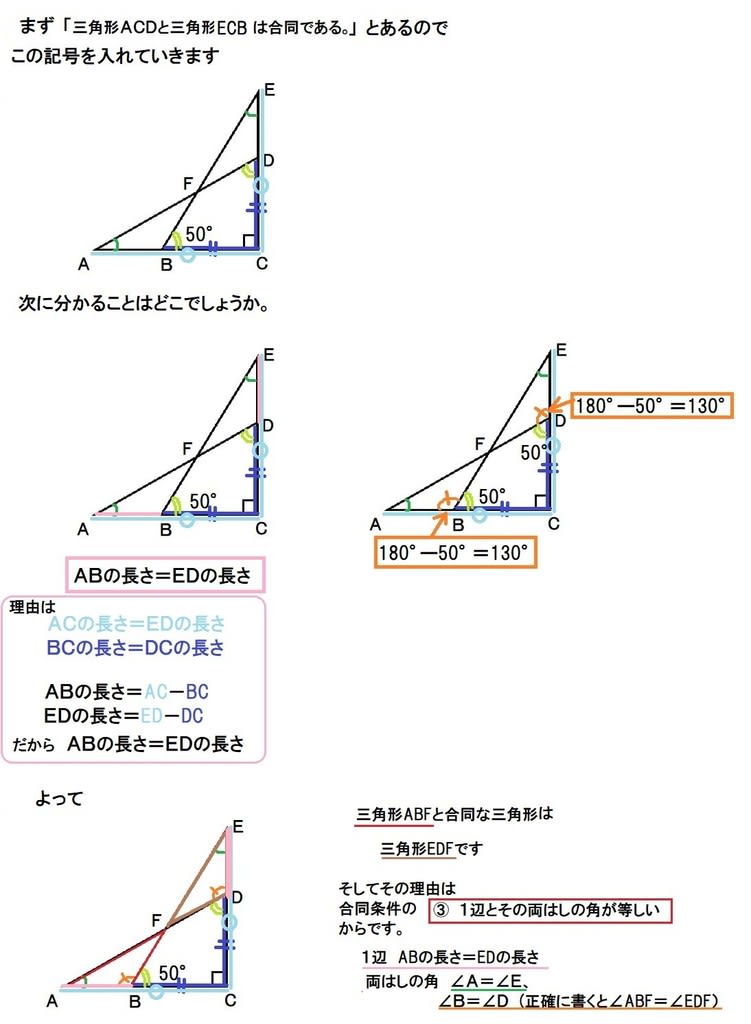



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support



Http Www Fdtext Com Dan Fdn S2 05 Goudou Pdf




中学数学 図形の合同 図形の性質




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
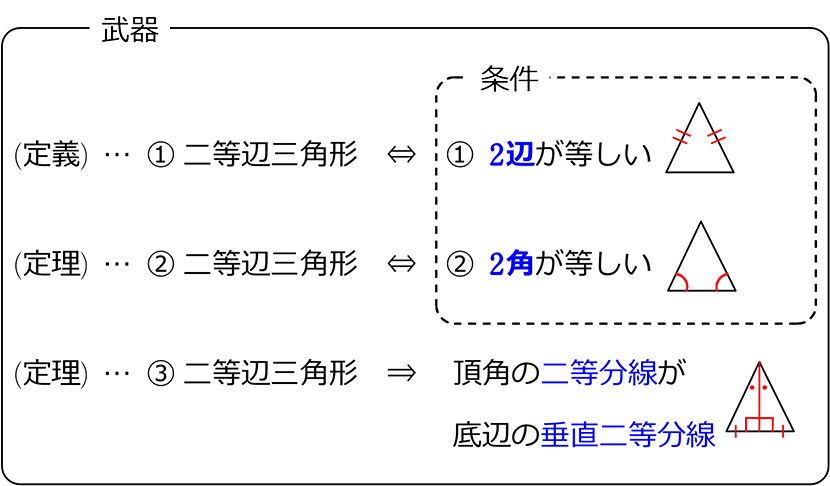



中学数学 図形の合同 図形の性質



Www Pref Shimane Lg Jp Education Kyoiku Kikan Matsue Ec Kyouiku Jhouhou Gakushushidouan Leader Kyouka Reader Math Data 25math2 Pdf




中2数学 三角形と四角形 章の問題a 赤城 ᐡᐤᐡ



中学数学 図形の合同 図形の性質



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典
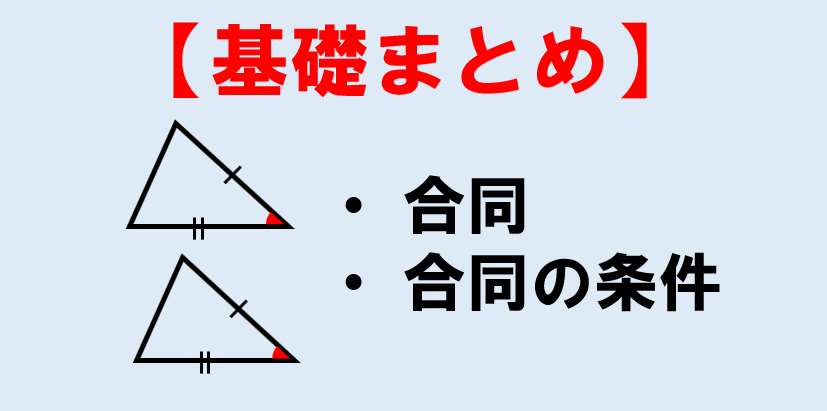



中2数学 合同 三角形の合同条件まとめ 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
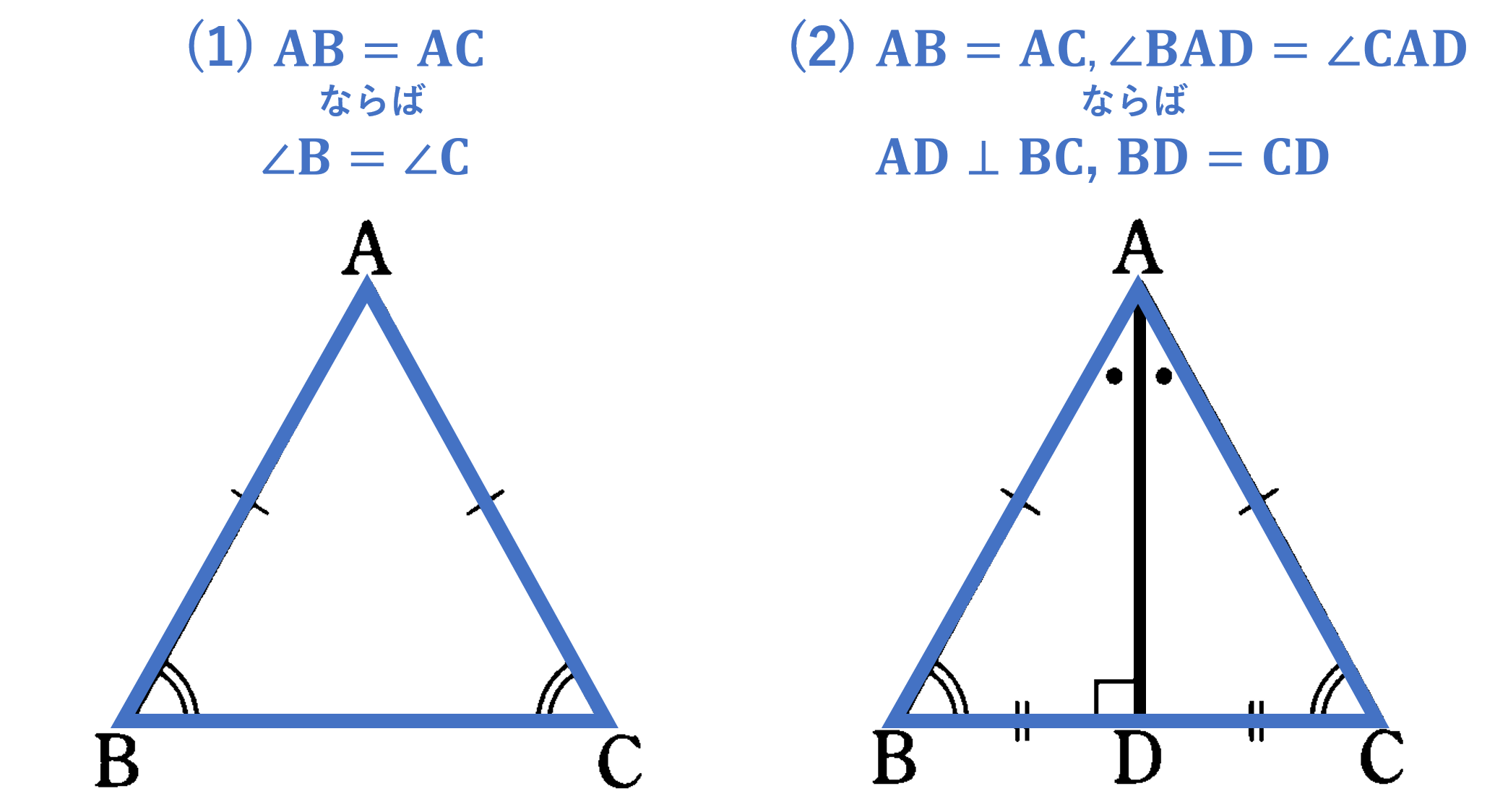



5章 三角形と四角形 タカラゼミ
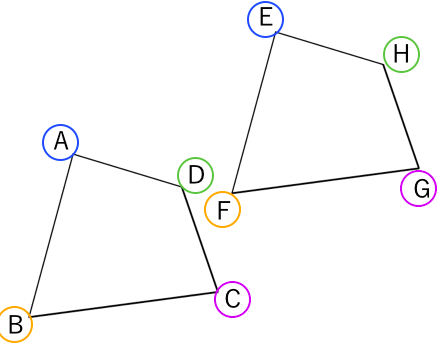



合同な図形とは 苦手な数学を簡単に
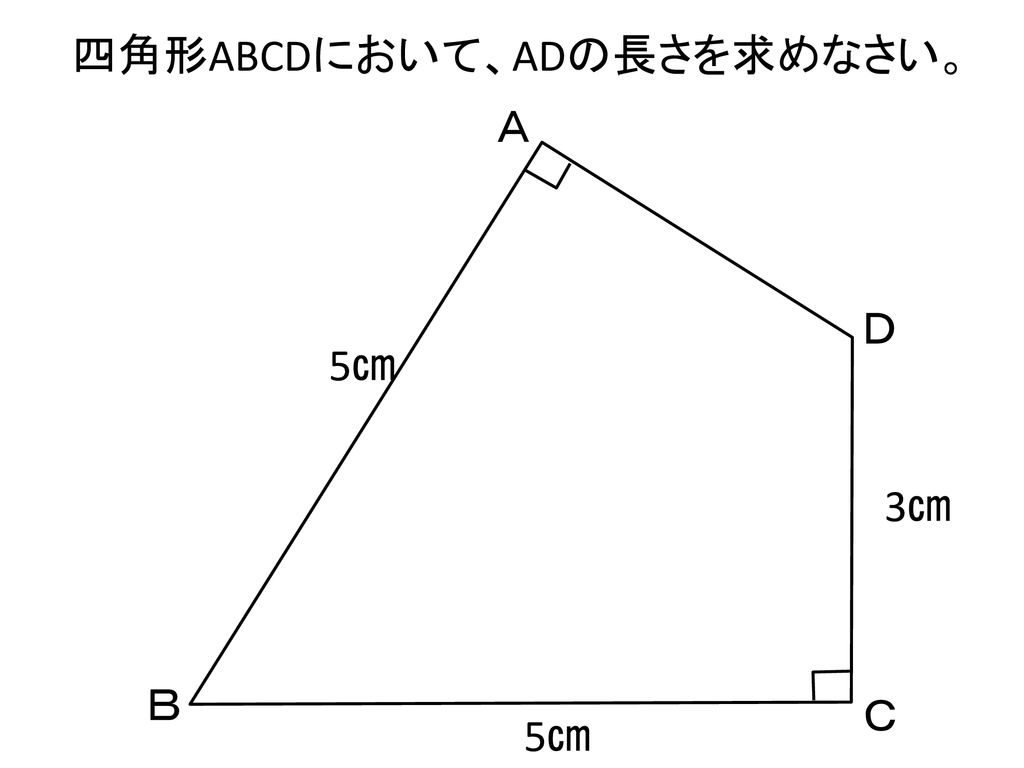



本時のねらい 直角三角形の合同条件を導き それを理解し 証明ができるようにする Ppt Download




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット




ねらい 平行四辺形の定義と性質を理解し 定義から導かれた性質を 三角形の合同条件などを使って証明することができる Ppt Download




5年算数 図形の角と合同 7 いろいろな方法で合同な四角形をかこう あなたの人生はあなたの思い描いたとおりになる
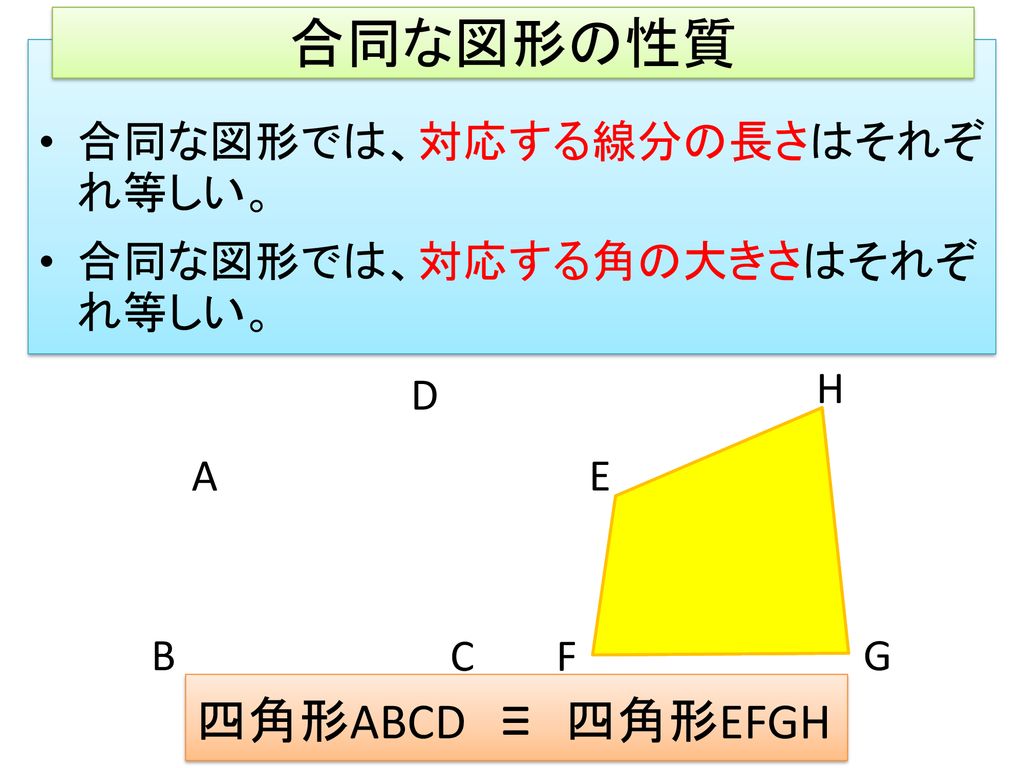



本時のねらい 合同な三角形の作図を通して三角形の合同条件を導き それを理解する Ppt Download



Http Www Impuls Tgu Org Cms Templates File Php Url 2fcms 2flibrary Pdf Files 2f122 2fsugekari15jp Pdf
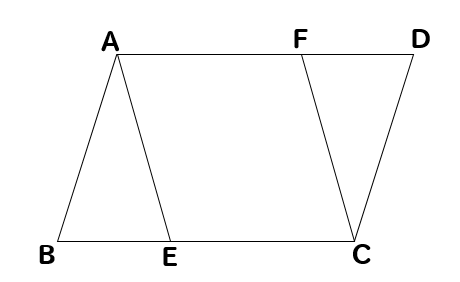



中学数学 平行四辺形の証明問題を徹底解説 数スタ




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット



中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
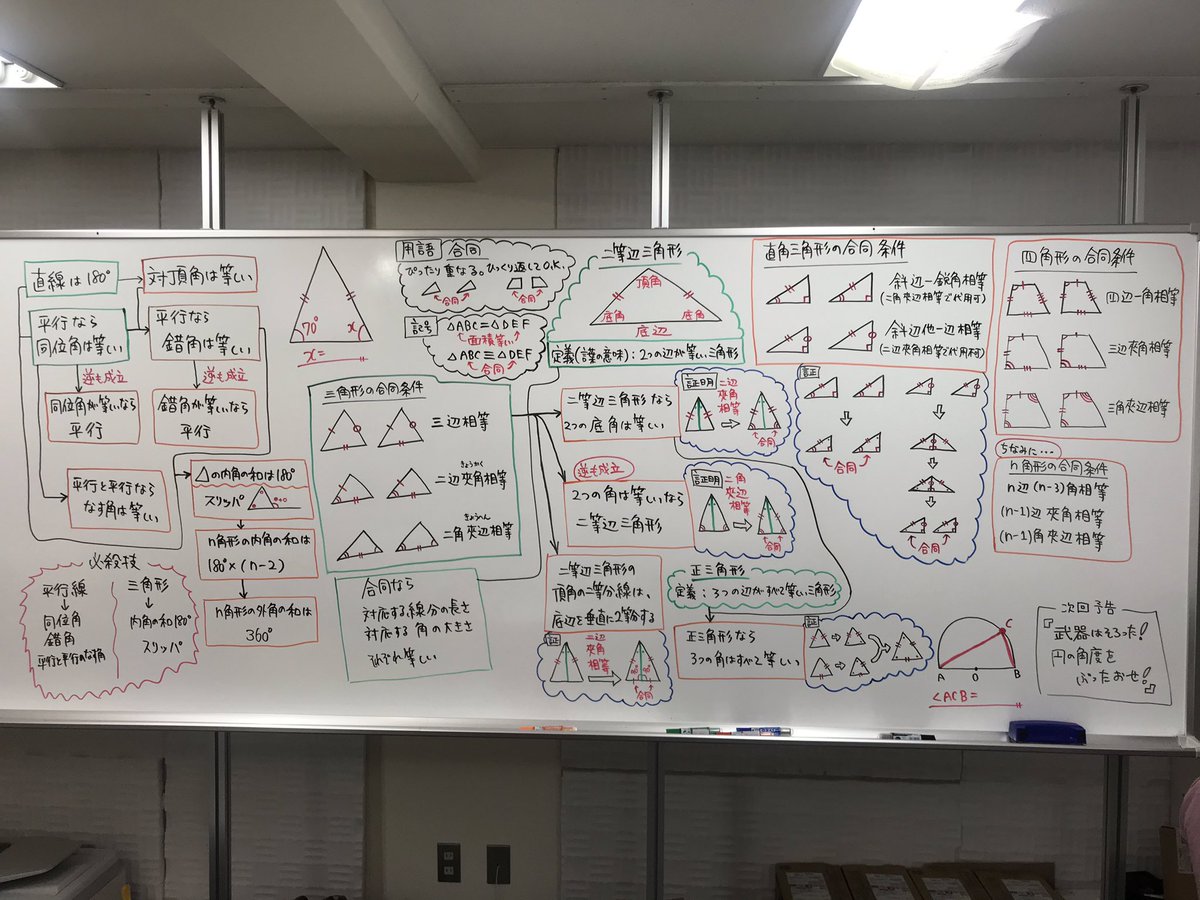



ট ইট র タカタ先生 所japan出演 スタフリ スタトモ 今日の授業動画は超自信作 昨日の動画で三角形の合同条件を紹介 今日の動画では 直角三角形の合同条件に加えて 四角形の合同条件 N角形の合同条件を 紹介しています N角形の合同条件を



四角形の合同条件について教えて下さい平行四辺形abcdの辺ad の中点をそ Yahoo 知恵袋



中学校数学 2年生 図形 図形の調べ方 Wikibooks



中学数学 図形の合同 図形の性質



Www Pref Shimane Lg Jp Education Kyoiku Kikan Matsue Ec Kyouiku Jhouhou Gakushushidouan Leader Kyouka Reader Math Data 25math2 Pdf



5章 三角形と四角形 タカラゼミ



三角形の合同条件 証明 中学2年 数学クラブ



Www1 Iwate School Jp Action Common Download Main Upload Id 1335



中学数学 図形の合同 図形の性質




5年算数 図形の角と合同 5 合同な四角形をかこう Youtube




中2数学 平行四辺形の証明 練習編 映像授業のtry It トライイット



1



平面図形の基礎




1 Descubre Como Resolverlo En Qanda
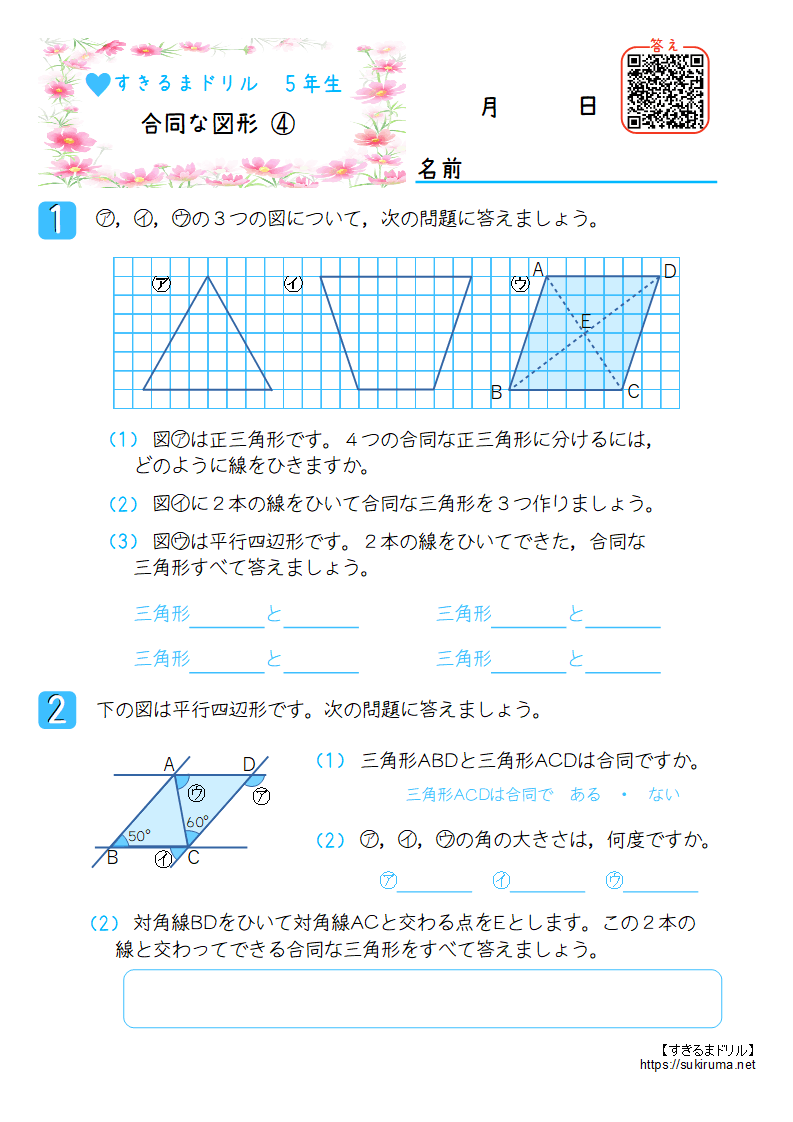



すきるまドリル 小学5年生 算数 合同な図形 無料学習プリント すきるまドリル 無料学習プリント




無料 中2数学 テスト対策 解答プリント 214 図形と合同2 三角形の合同
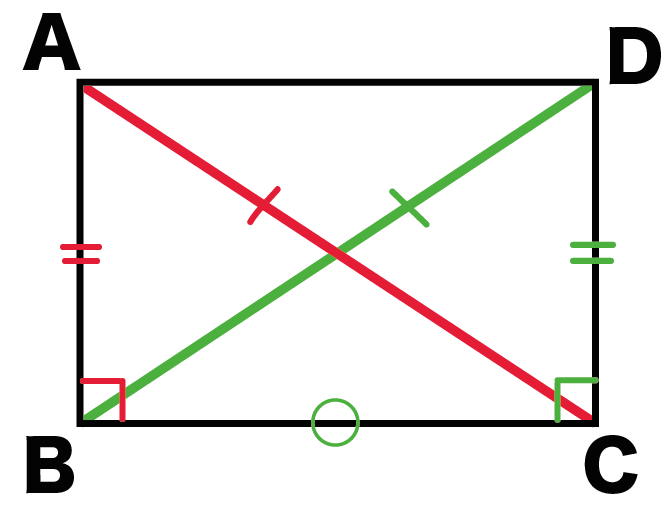



長方形の性質 対角線の長さはなぜ等しいのか Qikeru 学びを楽しくわかりやすく




数学 中2 56 三角形の合同 基本編 Youtube
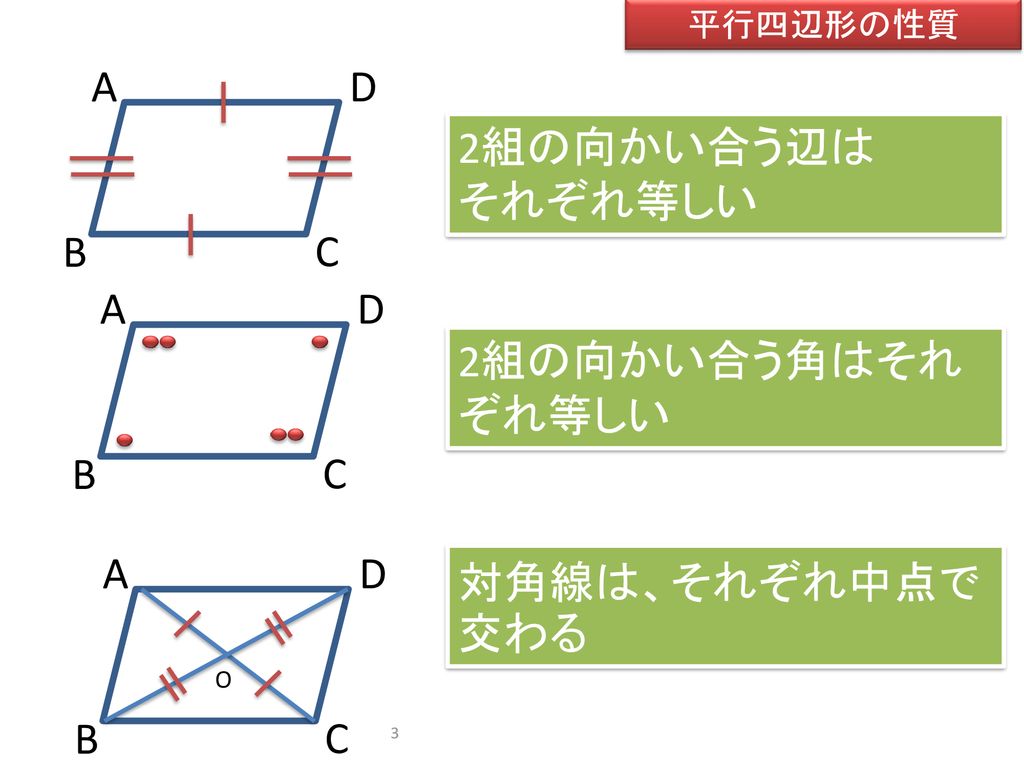



平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




無料 中2数学 基本解説 解答プリント 229 三角形 四角形2 直角三角形




三角形 四角形の証明です この回答ではダメですか 字きたないし画質も悪くてごめんな Clear



1



四角形の合同条件はありますか 4辺と1角がそれぞれ等しい3辺とそ Yahoo 知恵袋




三角形の相似条件と証明問題の解き方 数学fun
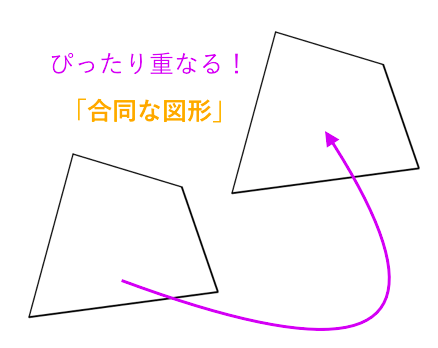



合同な図形とは 苦手な数学を簡単に




無料 中2数学 発展問題 解答プリント 228 三角形 四角形1 二等辺三角形




数学 中2 74 平行四辺形になる条件 Youtube




中学校数学 2年生 図形 三角形と四角形 Wikibooks



数学教育 07年5月号 平面図形 四角形の合同条件を考える



高校入試 英語 数学 学習 三角形と四角形 直角三角形
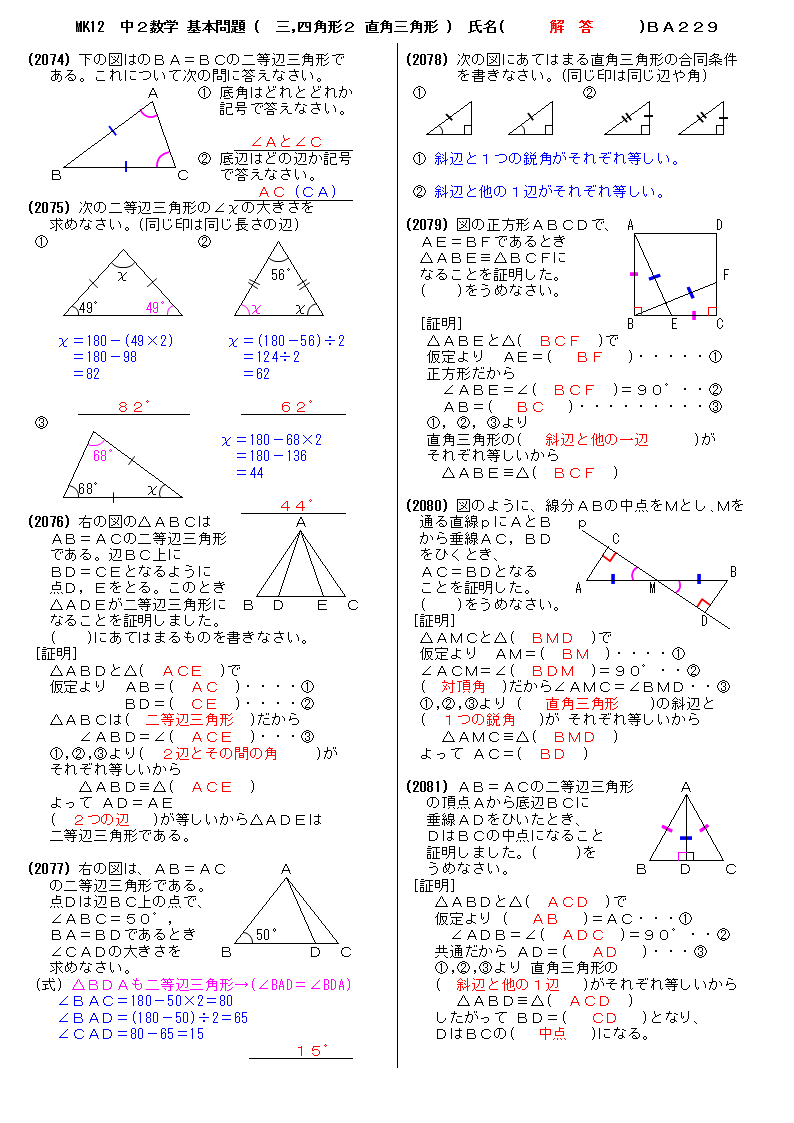



無料 中2数学 基本問題 解答プリント 229 三角形 四角形2 直角三角形




こーゆー問題のかんたんな考え方教えてください Clear
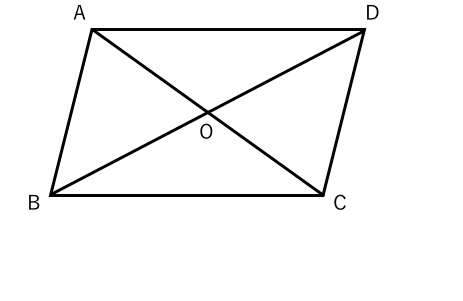



合同な三角形 平行四辺形で証明 苦手な数学を簡単に



四角形 五角形の相似 合同条件を教えてください 確か 中学の教科書に書 Yahoo 知恵袋



数学教育 07年5月号 平面図形 四角形の合同条件を考える




中2 数学 中2 証明 中学生 数学のノート Clear



Http Www1 Center Spec Ed Jp D H18 H18 Da08 Sansuu Suugaku Pdf Zukei Zukei 3 Pdf




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット



Www Kyoiku Kensyu Metro Tokyo Jp 08ojt Helpdesk Plans Chu Files Su 28 2 1 Plan Pdf




中学数学 図形の合同 図形の性質



四角形の合同条件について 二つの四角形を それぞれその対 Yahoo 知恵袋



四角形の合同条件について できるだけやさしく教えて下さ Yahoo 知恵袋



Math 平行四辺形 平行四辺形になることの証明 働きアリ The 2nd




中2 数学 証明に使う条件 性質まとめ 中学生 数学のノート Clear



Www Mext Go Jp Component A Menu Education Detail Icsfiles Afieldfile 0427 Mxt Kouhou02 084 Pdf
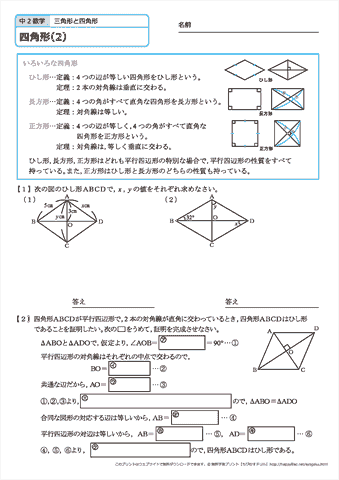



中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中2 四角形の合同証明 中学生 数学のノート Clear
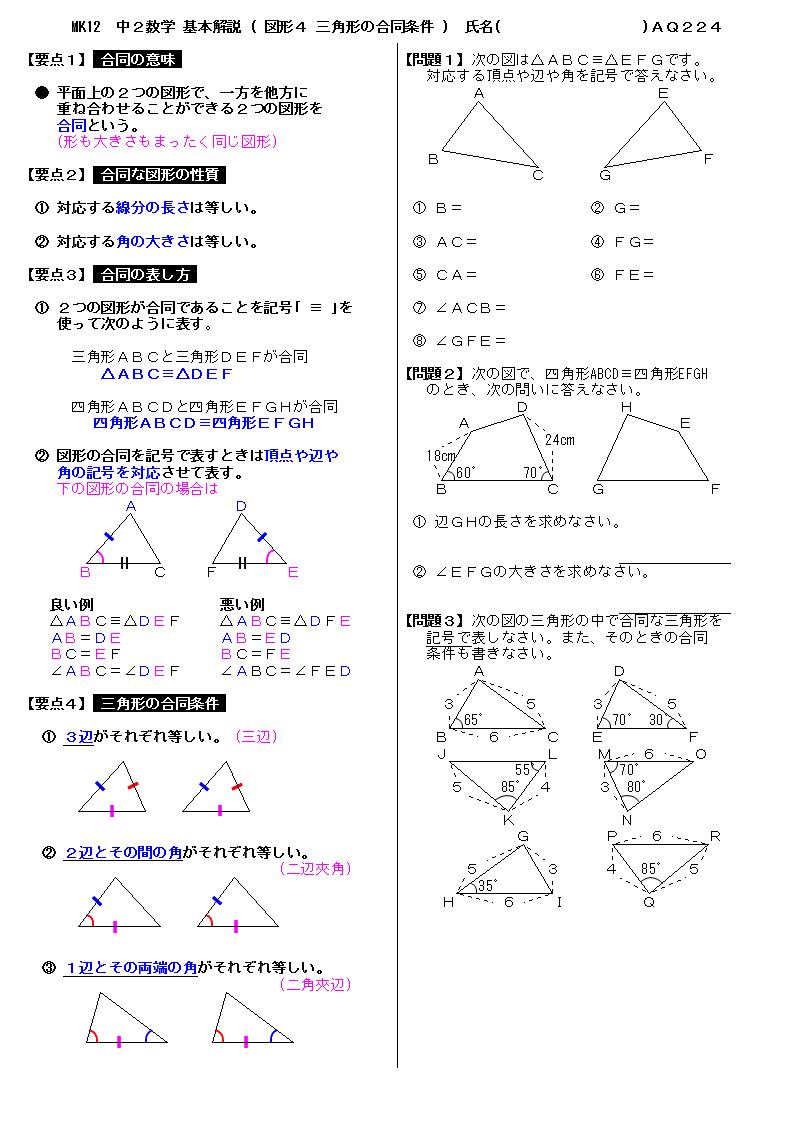



無料 中2数学 基本解説 問題プリント 224 図形4 三角形の合同条件




Math 平行四辺形 平行四辺形になることの証明 働きアリ
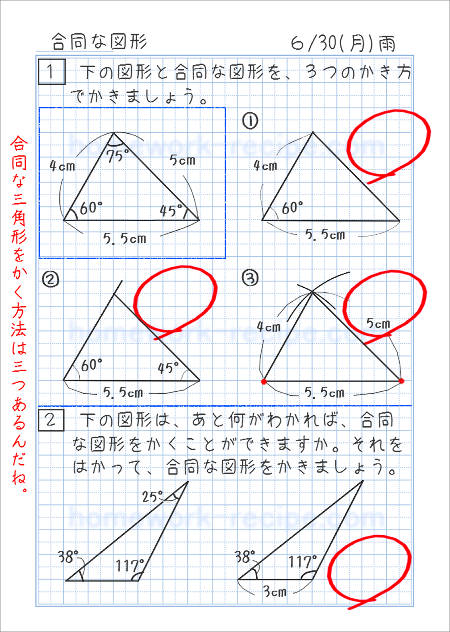



合同な三角形をかこう 家庭学習レシピ




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




Square 1 下の 四角形 Abcd2 と合同な四角形を アキ から クァンダ Qanda で解き方を見る




長方形 ひし形 正方形の性質と条件 Youtube
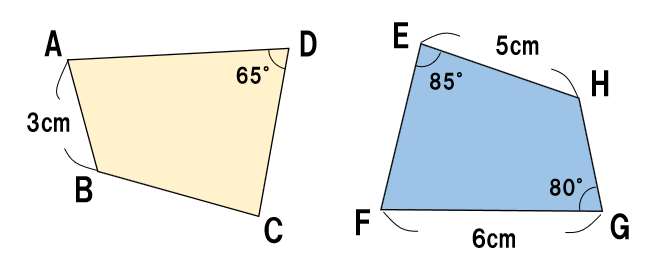



中2数学 合同 三角形の合同条件まとめ 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト



学校や塾であまり教えないが 受験に必要な知識 3 四角形の分類 中学受験 算数 虎の巻 東京 駒込 進学塾サクセス 塾長ブログ
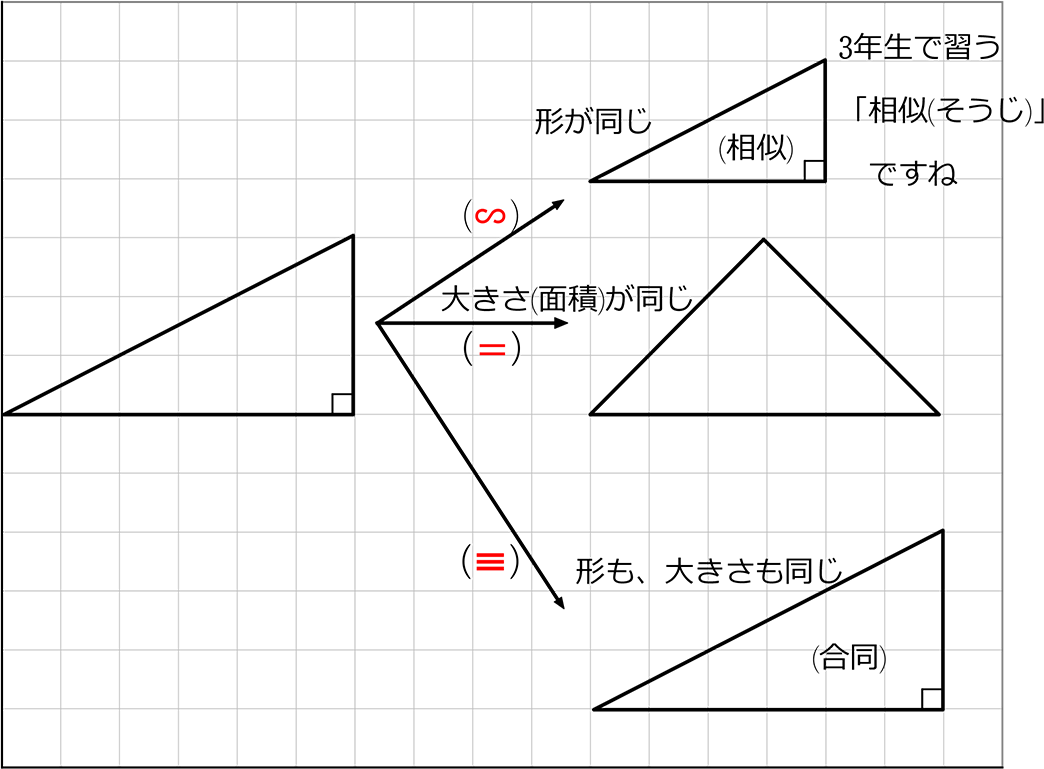



中学数学 図形の合同 図形の性質



Http Www Hrs Kaita J Ed Jp Learninginnovation H30 H31sugakugoudoujokenkawamoto Pdf


