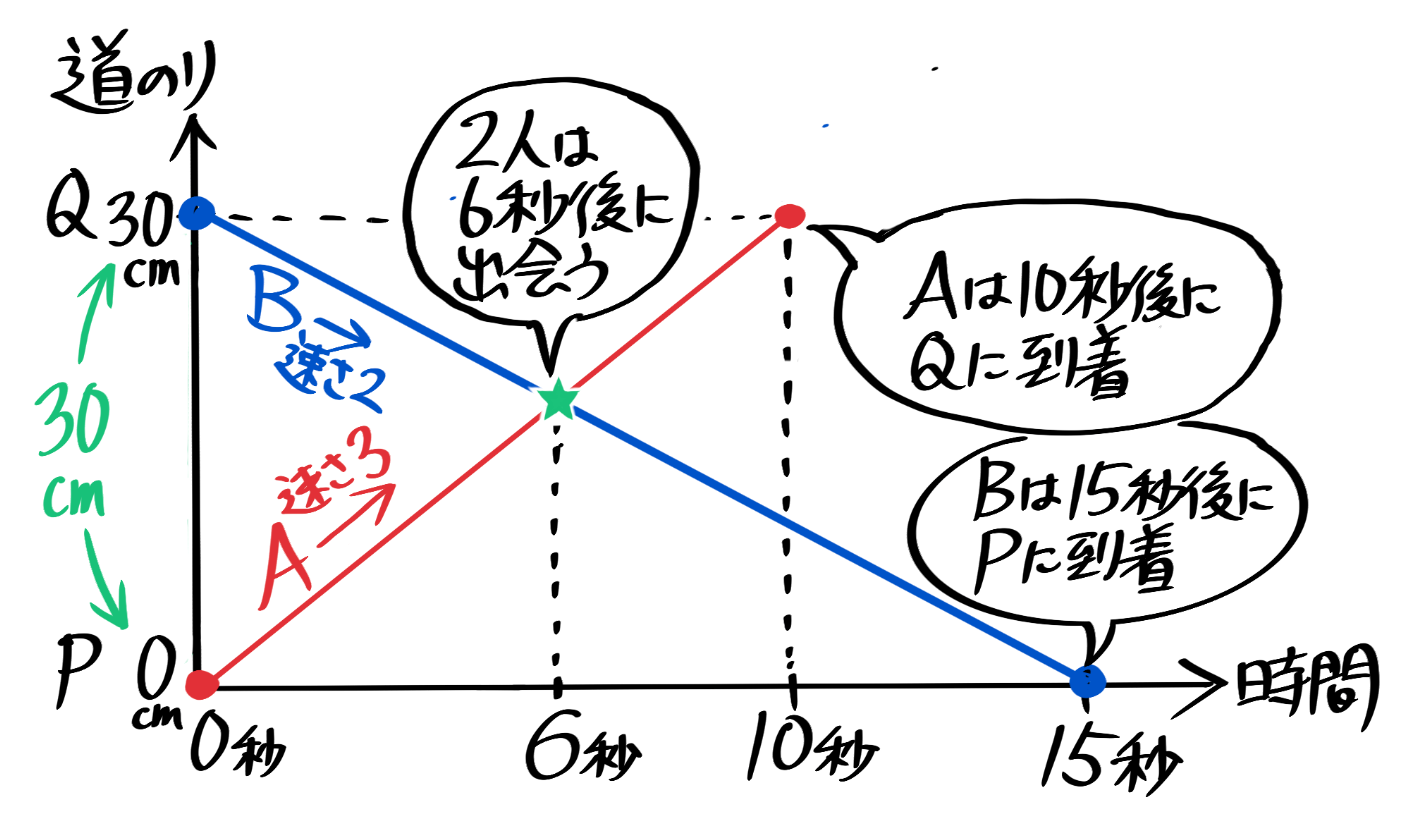
「速さ」の単元は、中学受験の算数では 四天王のひとつ と言っても過言ではありません。 ここで、「速さ」のジャンルの問題や使う技をあげてみましょう。 速さの三公式 平均の速さ 旅人算 流水算 通過算 時計算 図形上の点移動 水量変化<旅人算とグラフ(ダイヤグラム)> 右のグラフは,A町とB町の間を毎時30 kmの速さで往復するバスのようすを表したものです。四谷君は7時にA町を歩いて出発し,8時40分にB町に着きました。 (1) 四谷君の歩く速さは毎時何kmですか。 そうちゃ式 受験算数(2号館 図形/速さ) pを出発地qを目的地にしているので、pからqに向かうaのグラフは右上がりに、qからpに向かうbのグラフは右下がりになります。 aとbがさらに進んで、それぞれq、pに着くまでを考えてみましょう。 aは出発から30÷3=10秒後にqに到着し、bは30÷2=15秒でpに到着

中学受験 算数 数量編
中学受験 算数 速さ グラフ
中学受験 算数 速さ グラフ- 旅人算とグラフ 中学受験準備のための学習ドリル 16年6月3日 / Last updated 17年9月25日 doramaru 算数 速さ中学受験各教科(国語・算数・理科・社会)の勉強法 (1) 勉強ができない3つの理由 (1) 問題文の中に答えの半分はある!



中学受験のための学習プリント 小学生無料プリント 算数問題 国語問題 ドリル
テキストは四谷大塚にてお買い求め下さい。 著作権は中学受験の算数・理科ヘクトパスカルに帰属します。 転載または、商用での無断使用を禁止します。 予習シリーズ手書き解説の コース名と価格表 予習シリーズ手書き解説の お申し込みについて プロ家庭教師集団「名門指導会」算数科主任の高野健一です。 入試に向けて算数で特に押さえておきたいポイントについてお話しする3回シリーズ、前回は 図形問題を解くポイント を紹介しました。 2回目の今回のテーマは「速さ」です。 中学入試の算数において、「速さ」は出題頻度の高い分野の1つです。 その一方で、速さを苦手とする子は少なくありません 反比例のグラフは以下です。中学受験の算数ではあまり比例・反比例をじっくり扱わないので、知らない子もいます。ぜひ覚えてください。 反比例の代表例は「ピストンに閉じ込められた空気にかかる重さと空気の体積」 横軸:重さ 縦軸:空気の体積 重さが2倍3倍になると空気の体積
21年1月19日 入試解説と分析 テスト速報, 入試分析・志望校別対策 この記事では、21年東大寺学園中学入学試験について、受験者数・平均点・合格最低点をご紹介した上で、1月18日の試験(算数)の問題PDF、プロ講師による所感・問題別難易度分析・一部問題の解説動画を掲載しております。 本試験を受験されたご家庭や東大寺学園中学志望者にとって、21年の中学受験算数解法1000→「イメージでわかる中学受験算数」 18年10月 4日 (木) 日記・コラム・つぶやき, 中学受験, 算数, クイズ, パズル, 速さ, 表とグラフ 固定リンク コメント (0) トラックバック (0) 18年1月 5日 (金) ①、②、③にあてはまる数は?(海城中学 17年)二つの直角三角中学受験 算数プリントの主な内容 和差算 植木算 周期算 分配算 方陣算 展開図と見取図 等差数列のしくみ 円と多角形 割合の利用 百分率と歩合 消去算 代入算 円とおうぎ形 つるかめ算 平均の面積図 食塩水の問題 場合の数 ならべ方 数の性質 素因数分解とn進法 差集め算 旅人算 合同と相似 通過算 時計算 仕事算 ニュートン算 流水算 条件整理と推理の利用 立体と投影図
速さと比 (旅人算の基本) では進行グラフの基本的な使い方を確認しましたが,このページでは進行グラフそのものを問題としている代表的なパターンを紹介します. まずは1問目です. 問題1:下のグラフのように,AとBの間を2台の車P,Qが一定の速さで進みました.PとQが出会った時刻は何時何分何秒ですか. グラフを見てもA―B間の距離はわかりません.よってP 中学受験算数の速さ問題を禁断の技で解いてみる 私は "中学受験未経験父ちゃん" です。 中受算数の速さ問題をネット検索して調べたら、小学生ですんげぇ難しい問題解くんだなってびっくりしたお。 とりあえず、浮かび上がってきたポイントは、 1.一定のものを探す。(速さ ベネッセ中学受験ニガテ単元を克服し、親子で合格力アップ!。 子育て・教育・受験・英語まで網羅したベネッセの総合情報サイト HOME> 受験> 中学受験> 中学受験 受験対策 基礎知識;



グラフから速さを求める 中学から数学だいすき



変化のグラフ 中学受験ブログ
(1) 大項目から小項目へ (1) 目標を達成する科学的方法 (1) 繰り返す+間違え グラフを読み取る旅人算(中学受験算数 変化とグラフ) バスに乗っていた時間は?(中学受験算数 速さ) ややこしい速さの問題(中学受験算数 速さ) つるかめ算の入る速さの問題 時間が同じ場合の速さと距離(智弁学園和歌山中学 10年) グラフと速さ(国府台女子学院中学部 10年) グラフを読み取る力(桜蔭中学 11年) 芝中学校07年度 算数入試問題 速さのグラフ (1)解説解答 兄と弟の歩く速さはそれぞれ分速何mですか。 解説 兄がA地点から、弟がB地点からそれぞれ往復するときの様子は下図の通り AB間0mを同時に出発して、2人がはじめて出会うのは2分後なので、2人の



旅人算とグラフ 1 中学受験 田中貴 Com



1
A地~b地(中学受験算数 グラフと速さ) (1)の結果を使う(2)(中学受験算数 点の移動) グラフの形(中学受験算数 基本形だ問)みんなの算数オンライン 中学受験 5年 速さ・旅人算 速さとグラフ・ダイヤグラムグラフを読む 第27問 速さと比 (芝中学 受験問題 13年(平成25年度) 算数) 速さ 第70問 流水算 (海城中学 受験問題 13年(平成25年度) 算数)




流水算の練習問題 応用編 速さの比やグラフも登場



1
「速さの三公式」「進行グラフの読み取り方」という算数の要素だけでなく、 「予定の時刻にb君の家に着く」という部分の 題意を把握する力も 必要 だ とわかります。 中学入試問題では 中学受験・算数の出る順ランキング6位 場合の数 (リンク先にそれぞれの解説・問題があります) ・図形と場合の数 ・並べ方 ・組み合わせ ・数の性質と場合の数 ・サイコロ、じゃんけんの問題 中学受験・算数の出る順ランキング7位 グラフ・調べと推理 グラフ 受験算数 比 水そうとグラフ 立体図形 算数応用 速さのいろいろな問題 ;



速さの問題 中学受験 田中貴 Com



みんなの算数オンライン 中学受験 5年 速さ 旅人算 速さとグラフ ダイヤグラム 例題と解説
第493回 合否を分ける問題の解き方 点の移動とグラフ これまで、中学入試の合否を分ける算数の問題として、「流水算」、「旅人算」という速さをテーマにした問題を見てきました。 今回は、 速さと図形の2つの分野が融合している「点の移動とグラフ」 を取り扱おうと思います。 「点の移動とグラフ」の問題では、グラフの読み取りが重要なポイントです。 その 旅人算:ふたりの距離のグラフ 中学受験 入試問題 解法テク 算数・速さ < 旅人算 >の< ダイヤグラム >に関連した問題で、出題者が正答率を下げたいと考えたとき、縦軸を「ある場所からの距離」から「ふたりの間の距離」に変えるだけで難易度がぐっと高くなります。 今日はこれの攻略法です。 例題は 大妻の10年 (平成22年)から大問の9 逆に言えば、出題者 速さと図とグラフ 速さの和(SAPIX 7月復習テストより) 速さとグラフ(SAPIX サマーサポートより) 電車と音の速さ(SAPIX ディリーチェックより) 速さとグラフ、通過算(SAPIX 8月マンスリーテストより) 速さと周期算(麻布中学 受験算数問題 09年) 速さと面積図(武蔵中学 算数入試問題 速さ) A地~B地(中学受験算数 グラフと速さ) 速さと道のり(開成



中学受験 旅人算とは 基本公式から往復など応用問題 ダイヤグラムまで そうちゃ式 受験算数 2号館 図形 速さ



中学受験算数の速さ問題を禁断の技で解いてみる 父ちゃんが教えたるっ
算数 桂川 紗織 中学受験点の移動のグラフを解くためのコツと無料プリント 中学受験の問題の中で、速さの中で「点の移動」という単元の学習があります。 点の移動は一般的に、旅人算を学習した少しあとくらいのタイミングで学習します。 点の移動の問題には、問題文だけでなく図やグラフがあり、それぞれに問題を解くための条件が少しずつ1から学ぶ中学受験算数シリーズ 第58回速さのグラフ(ダイヤグラム)①の授業プリント&授業映像 更新日: 年9月6日 中学受験の算数・理科を中心に書いて行きます。駒澤が旧字体なのは検索をしやすくするためです。 Sapix算数の単元リスト 中学受験 学習法と指導法 算数 Sapix授業の算数に関して小5と小6で登場する単元のリストを、声の教育社の中学入試過去問集での分類に準拠して作ってみました



桜蔭中入試の解体新書 過去問データに基づく算数傾向分析と対策 中学受験コベツバ




4月開始 中学受験算数の 問題 をとことん極めよう 算数表現力ゼミ 代々木オフライン教室 お試し1コマ受講 お申込受付開始 株式会社 Math Channelのプレスリリース
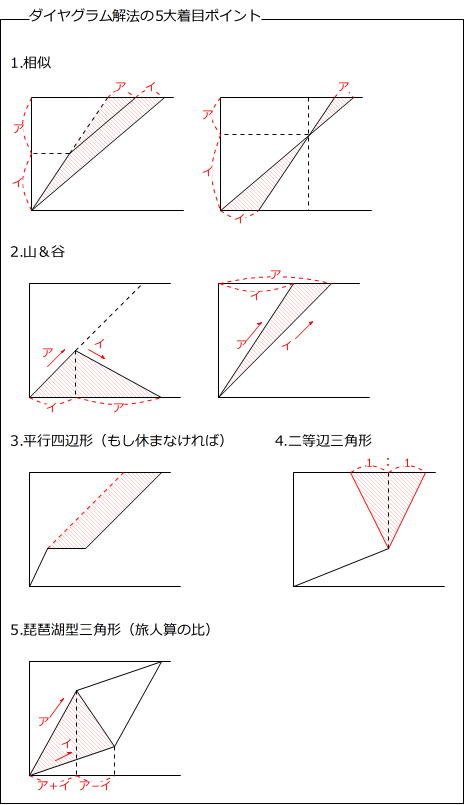
ダイヤグラムの基本的な着目点は、以下の5つです。 今回はこのうちの、 「相似(基本)」 について見ていきます。 はじめにご紹介する問題は、速さと比の典型問題のひとつです。 線分図解法、ダイヤグラム解法のいずれでも解くことができますので、 基礎の確認として取り組んでみることもできます。 16年度 雙葉中 入試問題 算数より 大問1 (3) A地点からB中学受験算数・高校受験数学けいたくチャンネル 98K subscribers Subscribe 中学受験算数「速さのグラフ(ダイヤグラム)②」小学4年生~6年生対象毎日配信A地~b地(中学受験算数 グラフと速さ) 速さと道のり(開成中学 06年算数入試問題) グラフを読み取る旅人算(中学受験算数 変化とグラフ) バスに乗っていた時間は?(中学受験算数 速さ) ややこしい速さの問題(中学受験算数 速さ)



苦手の克服 速さ5 前田昌宏の中学受験が楽しくなる算数塾



速さとグラフの問題 中学受験 田中貴 Com
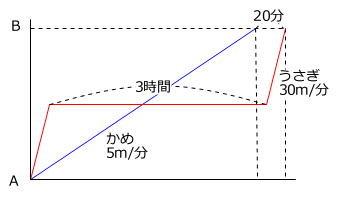
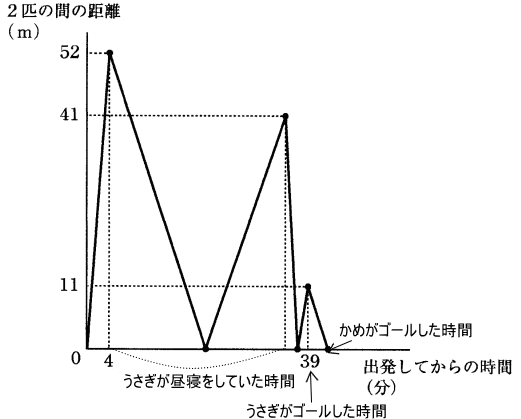
洗足学園中学校年度 算数入試問題 5速さのグラフ (1) 解説解答 (1) うさぎが昼寝をしていたのは何分間ですか。 グラフより うさぎが昼寝を始めたのは、同時に出発して4分後。 2匹の間の距離が52mになったとき。 うさぎが昼寝をしている間に亀は差を縮め、追いつき、さらに亀がうさぎより41m先に来たときにうさぎが再び走り始め亀に追いつき、さらに2匹の差が
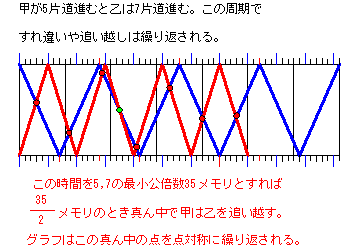



旅人算 往復経路 中学受験算数超特急シリーズ 無料版
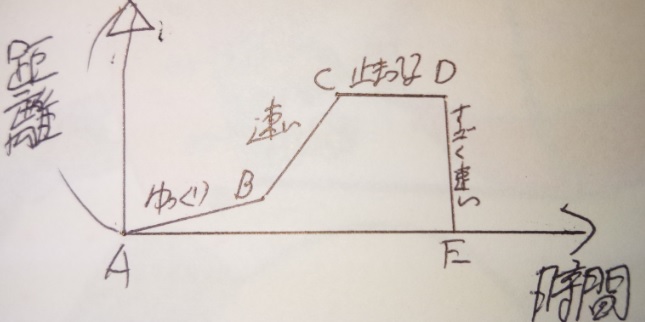



ダイヤグラムは速さのグラフ 相似 比率 逆比で読み解く 中学受験



1
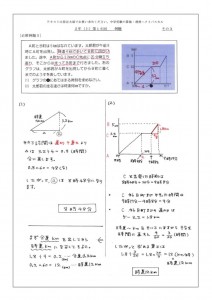



速さの問題 ダイヤグラム 進行を表すグラフ
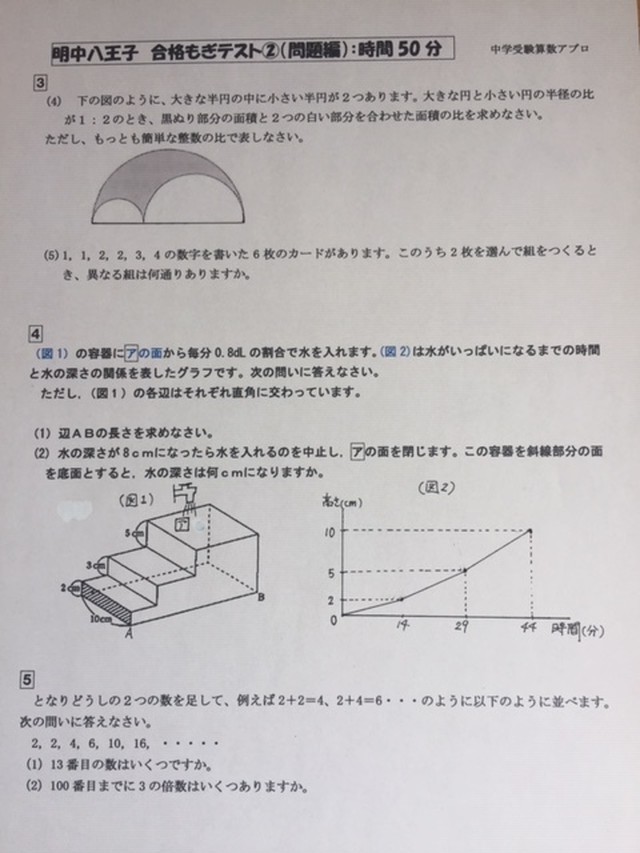



中学受験 明治大学付属中野八王子中学校 22合格への算数プリント アプロ中学受験算数プリント




算数 中学受験対策 図形の移動とグラフ 帰国生専門塾 大森ゼミナール



2




往復の平均の速さ 間違えずに求められますか




速さのグラフの問題 プロ家庭教師 俵屋の日記




算数ベストチェックの解説70 水そうグラフ 中学受験クルージング




算数 速さとダイヤグラム 中学受験 ベネッセ教育情報サイト
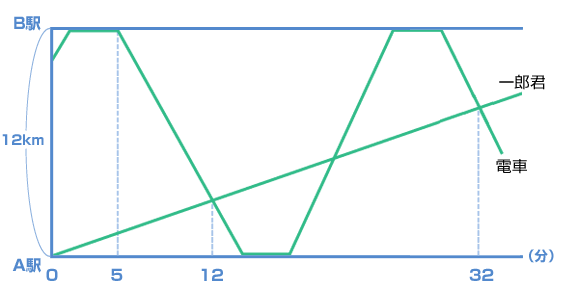



算数 速さとダイヤグラム 中学受験 ベネッセ教育情報サイト




速さと比 旅人算と進行グラフ 受験算数アーカイブス
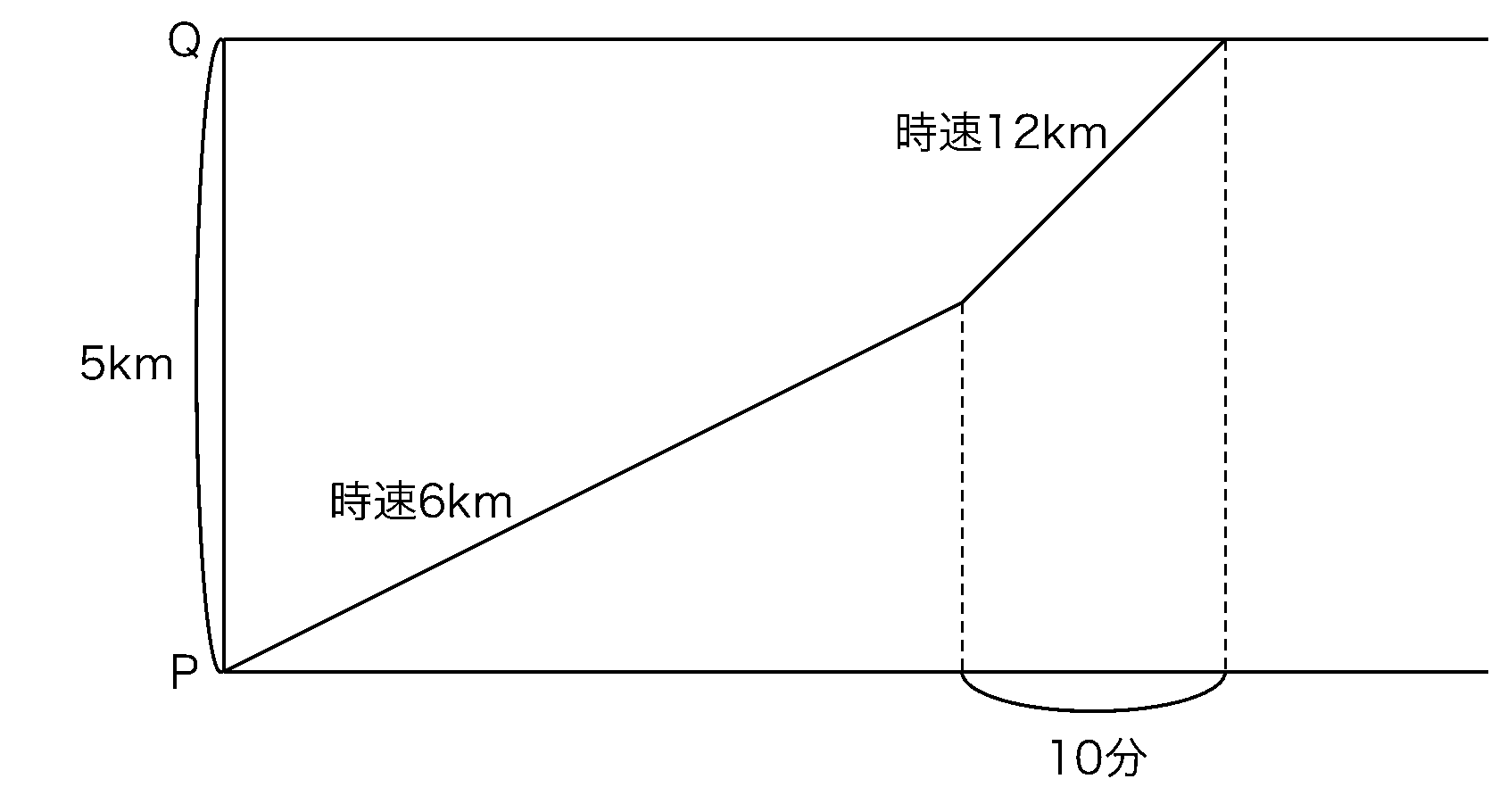



中学受験算数 ダイヤグラムの知られざる 利点 中学受験プロ講師ブログ




旅人算 ふたりの距離のグラフ 駒澤塾 中学受験の算数 理科



速さの文章題 中学受験 田中貴 Com




旅人算とグラフ 中学受験準備のための学習ドリル




旅人算とグラフ 中学受験準備のための学習ドリル
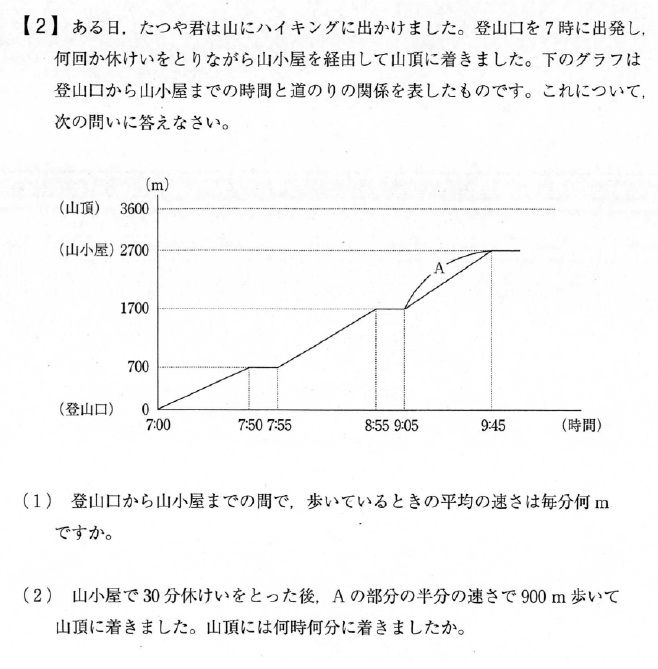



私立中 世田谷学園 10年入試 問題算数 第2問 速さのグラフ 過去問 解説あり 中学受験算数の全てが分かる 算数の森 ブログ版




中学受験 田園調布学園中等部 22合格への算数プリント アプロ中学受験算数プリント




中学受験 算数 数量編
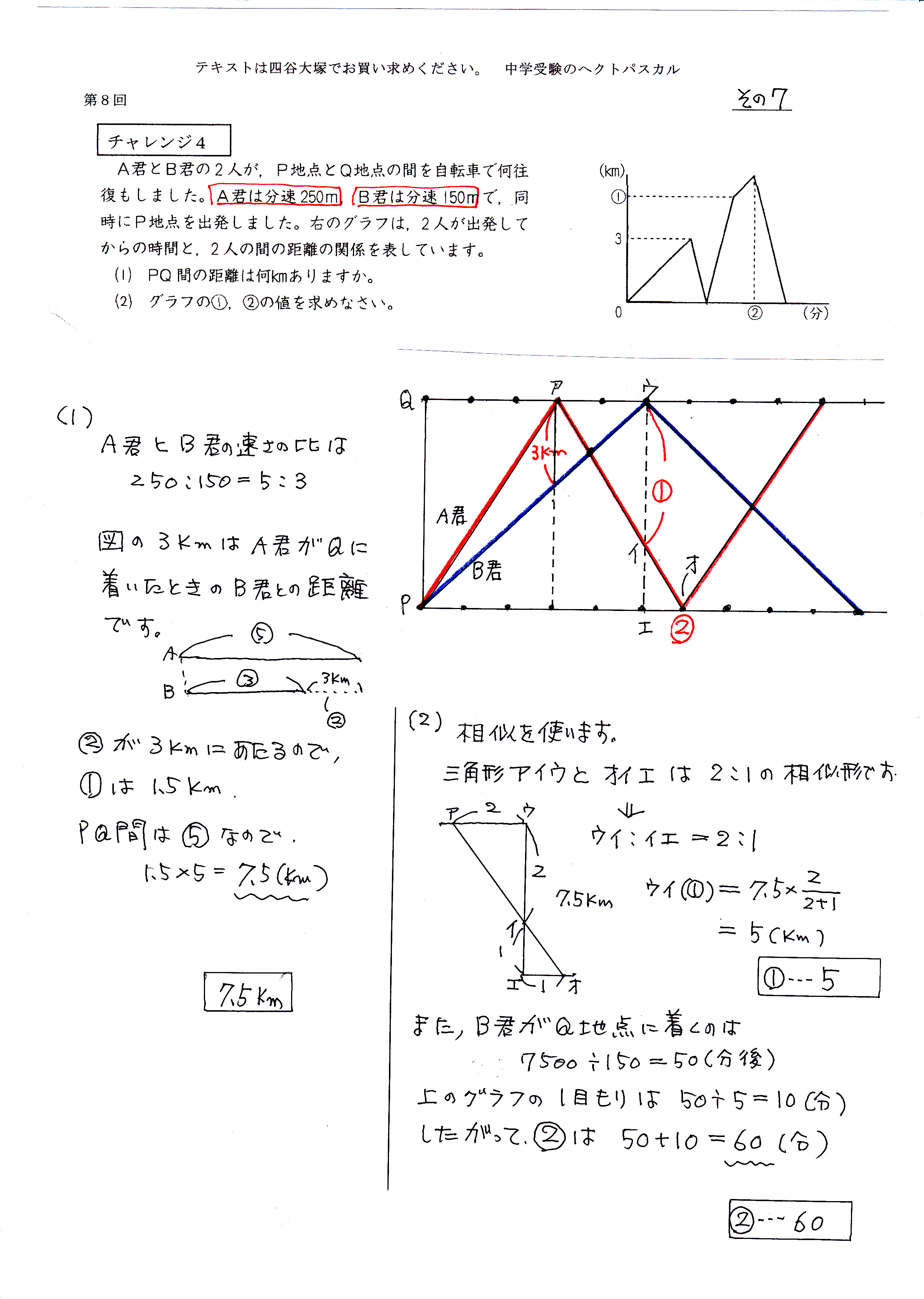



印刷可能 中学受験 算数 速さ 旅人算




ニュートン算 旅人算系の解法 駒澤塾 中学受験の算数 理科
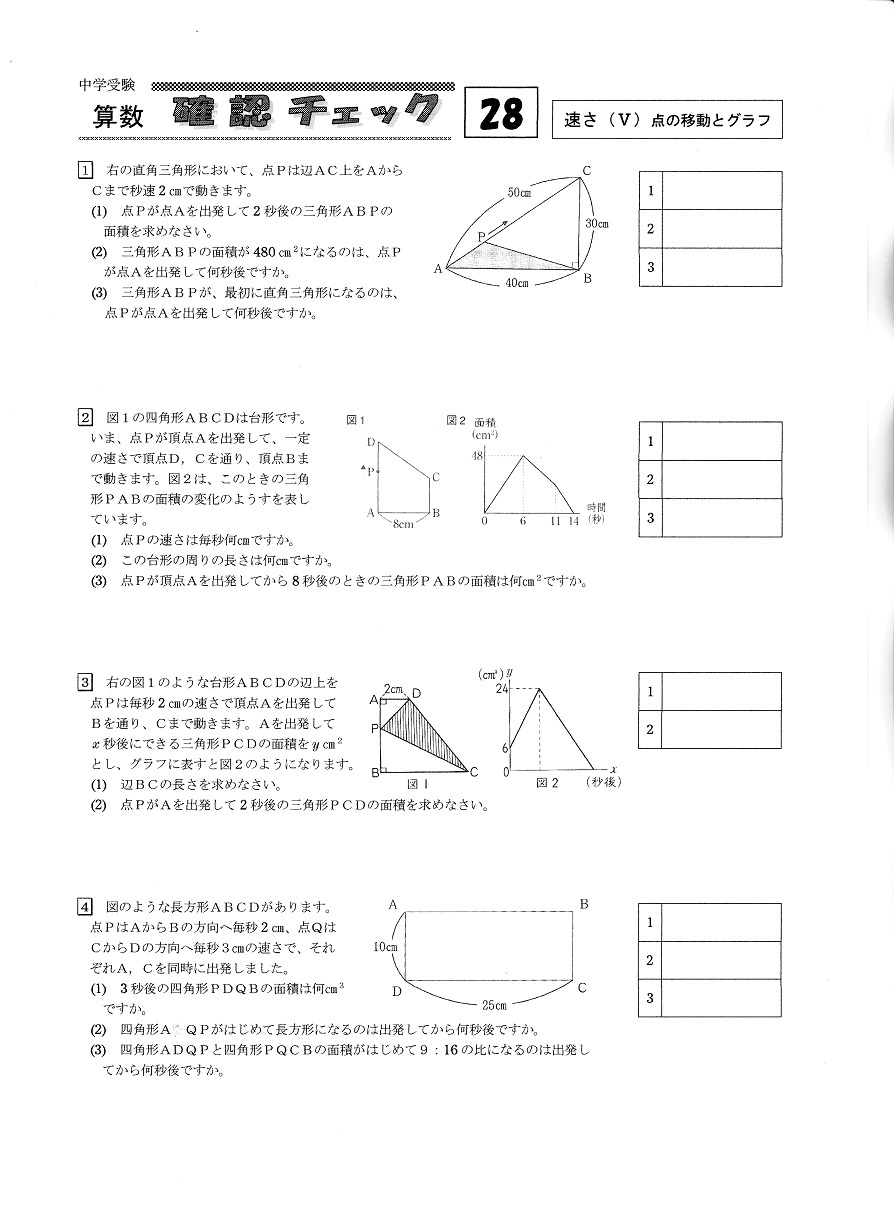



中学受験 算数確認チェック28 速さ 点の移動とグラフ グランパは元塾長



Lh3 Googleusercontent Com Proxy Tyfuytgjcvpgwitm3u0skhc9zzz4wiakm9cwjovg Wz3qkduba98m28awbjqxt4po Oou1hpki6u2aan5vt5aluqo6ut Zetqyog9tnc2fb1mw Pd3reox6rganvfoc8kfyxjfzxkrhpcweasoy1brqahpsyzm5e7c C37bnhctcfze54reozoj Uiiwv5tct2fi5nnw2msukvyj7qiqvd0frqumtldpurt




中学受験のための学習プリント 小学生無料プリント 算数問題 国語問題 ドリル



みんなの算数オンライン 中学受験 5年 速さ 旅人算 速さとグラフ ダイヤグラム トレーニング




中学入試の算数で速さの問題が得意になるには 中学受験専門 夏井算数塾



速さの比をグラフで読む名作問題 芝中学 2013年 どう解く 中学受験算数
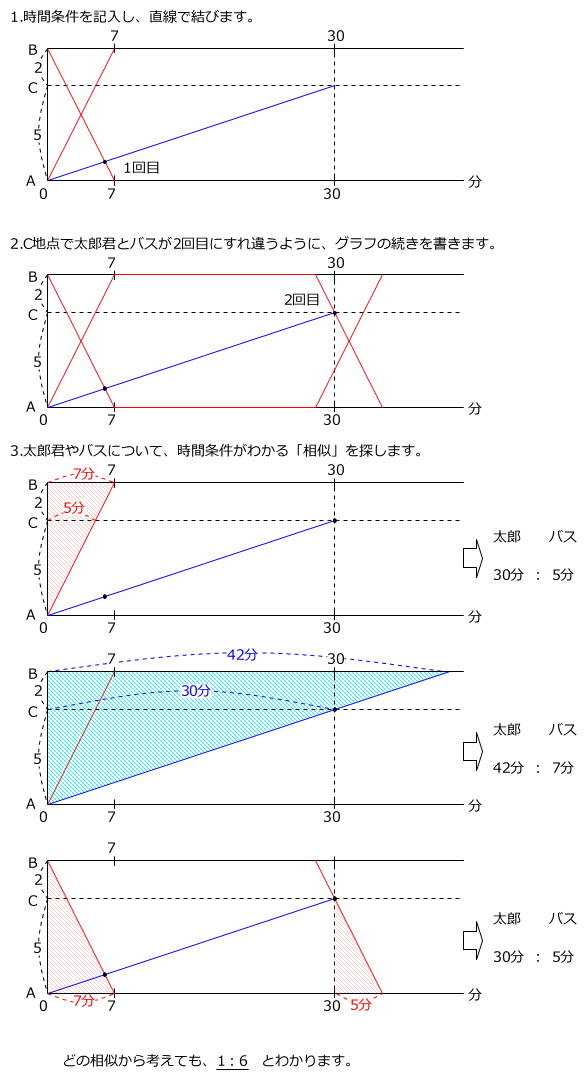



苦手の克服 速さ5 前田昌宏の中学受験が楽しくなる算数塾




速さ 速さのグラフ ダイヤグラム とは 中学受験算数 オンライン授業 数学 Spi Youtube




速さと比 旅人算と進行グラフ 受験算数アーカイブス




状況図とダイヤグラムどちらを書くべき 家庭教師としの勉強部屋




状況図とダイヤグラムどちらを書くべき 家庭教師としの勉強部屋




旅人算 Wikipedia



すぐるゼミ 小学生無料プリント 算数問題 国語問題 ドリル




神戸女学院中2019年 水問題ー 中学受験算数の良問 難問 基本問題
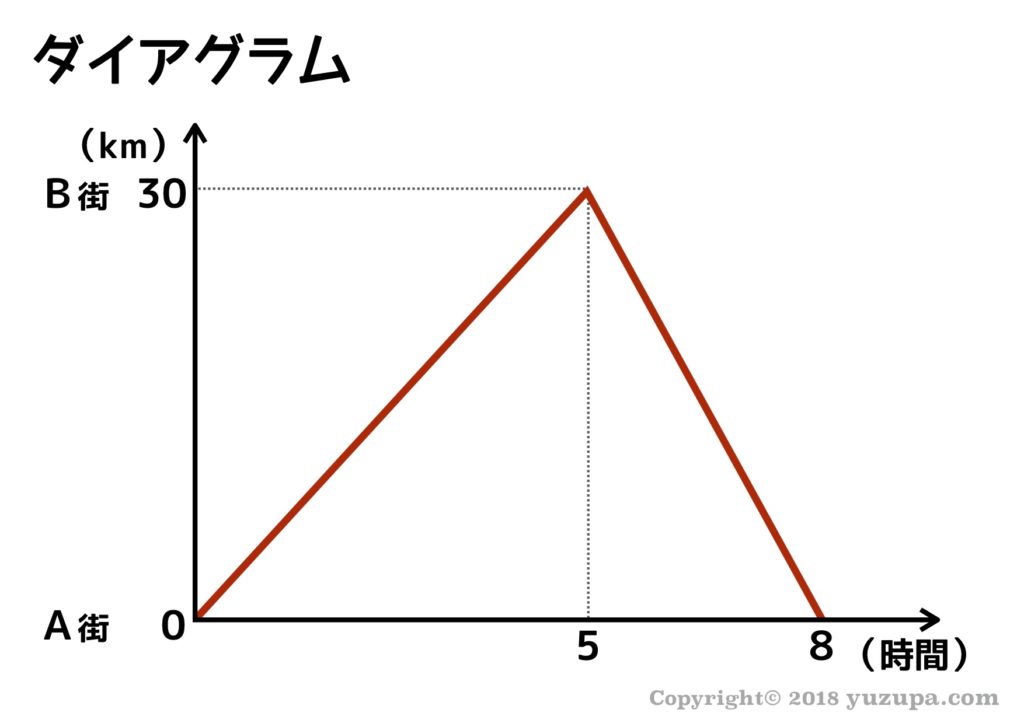



中学受験 流水算は 4つ速さを整理すれば簡単に解ける かるび勉強部屋



中学受験算数の速さ問題を禁断の技で解いてみる 父ちゃんが教えたるっ



速さ どう解く 中学受験算数




中学受験算数 速さのグラフ ダイヤグラム 小学4年生 6年生対象 毎日配信 Youtube
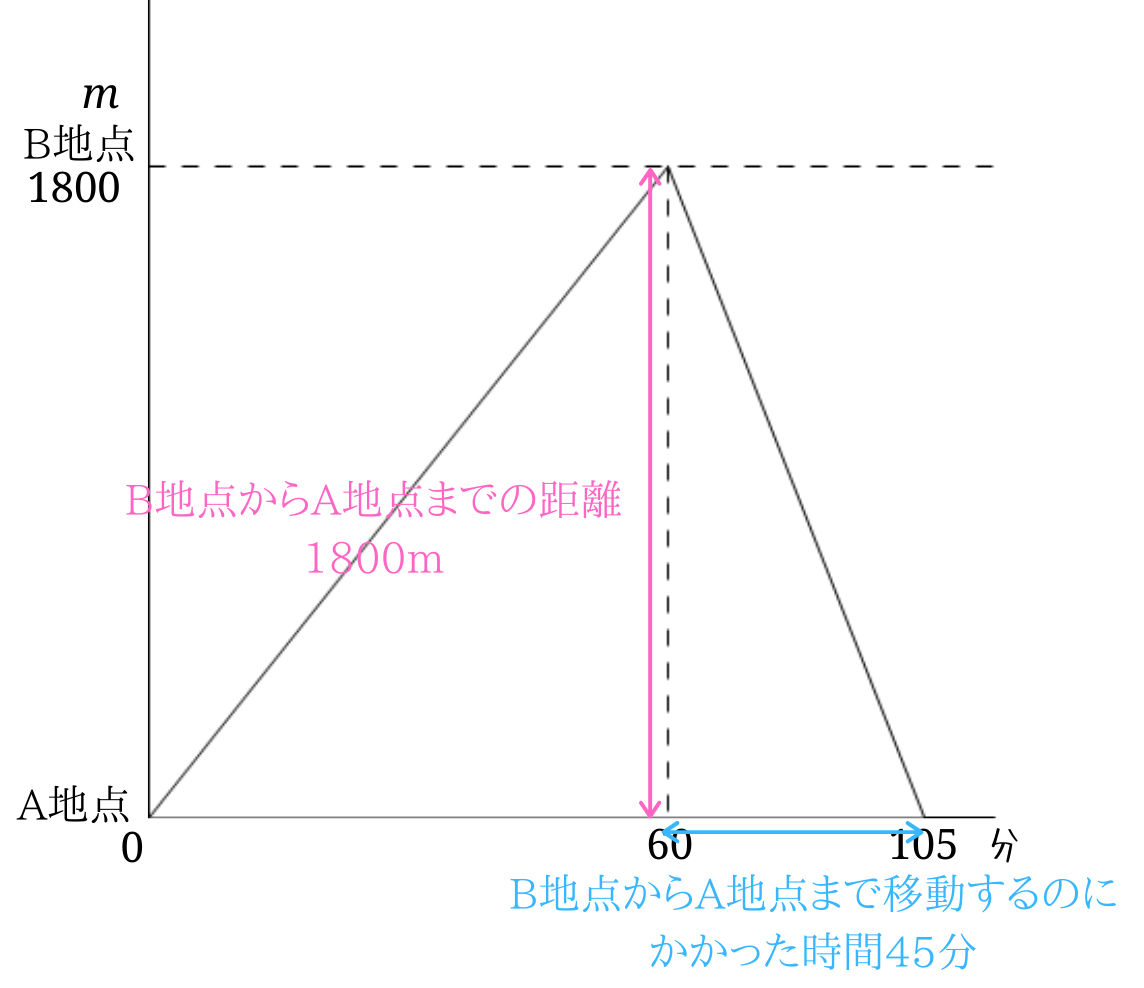



流水算が苦手をなくす解き方 教え方のコツは意外と簡単 ポイントはコレだけ みけねこ小学校
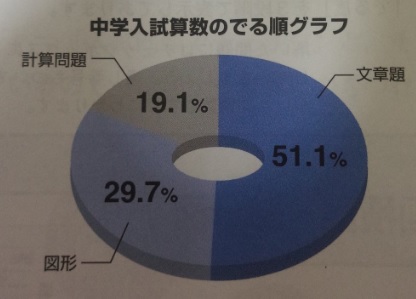



中学受験 算数の出る順ランキング7位まで 文章題ジャンル 中学受験




中学受験 算数の単元一覧 中学受験アンサー




中学受験 算数が苦手な子のための奥義 問題文の条件整理



受験算数とは 受験算数とメンタルサポートの中学受験専門プロ家庭教師アートオブエデュケーション Art Of Education



1




速さ 旅人算とグラフ2 算数教室 親子で学ぶ中学受験
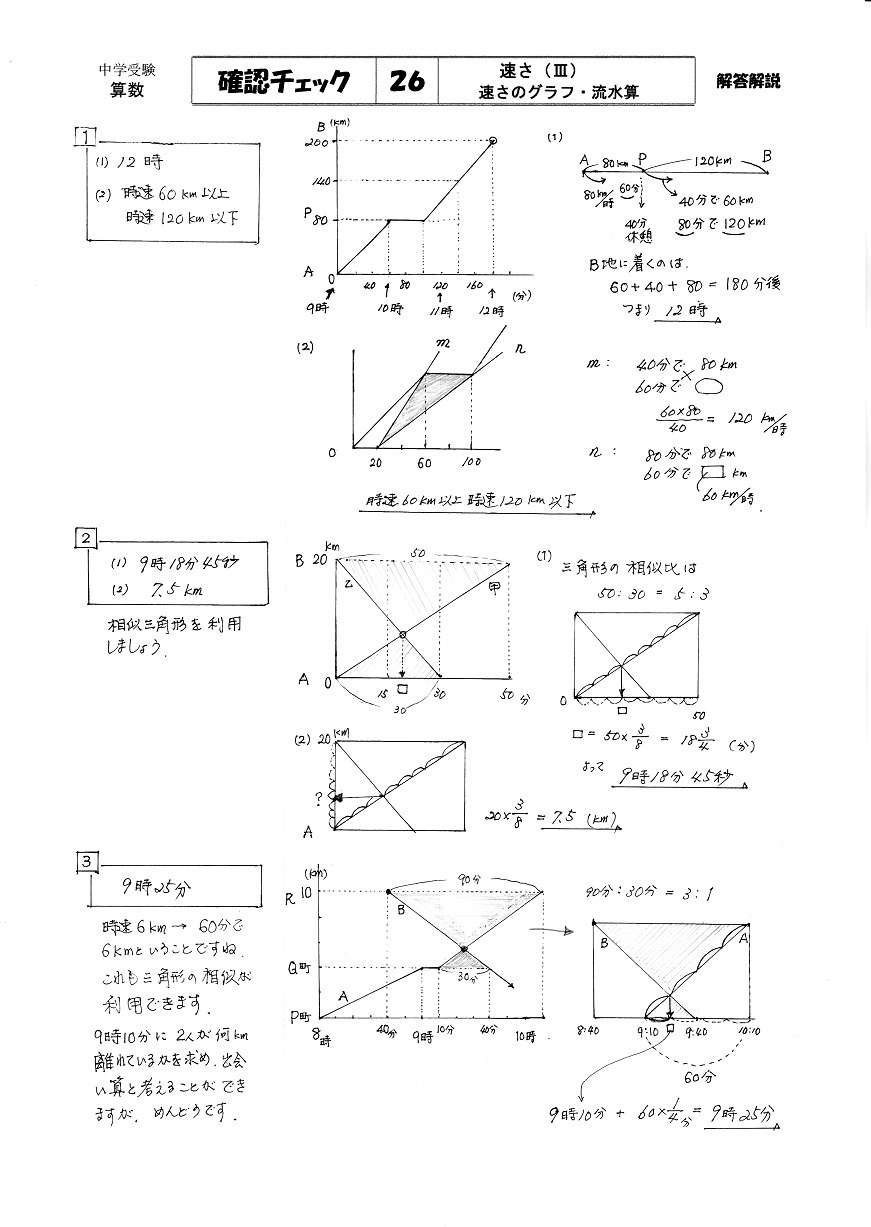



中学受験 算数確認チェック26 速さ 速さのグラフ 流水算 グランパは元塾長




算数 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




一次関数の利用 追いつく速さの文章問題を解説 数スタ




中学受験 点の移動のグラフを解くためのコツと無料プリント




水そうとグラフ 中学受験準備のための学習ドリル




小学6年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生
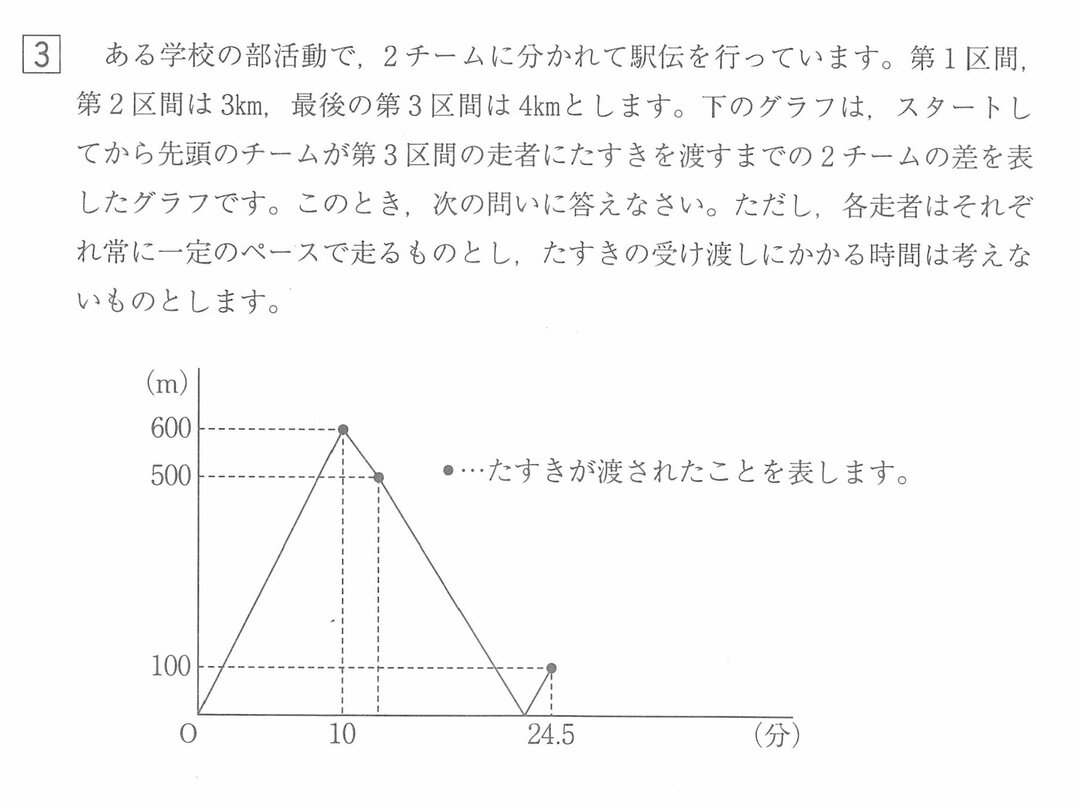



中高一貫校 入試算数の新傾向 埼玉 栄東 開智 の実際の問題から解読 完全版 中学受験への道 ダイヤモンド オンライン
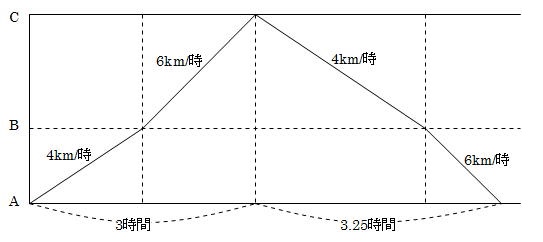



速さ 坂道の問題 14 前田昌宏の中学受験が楽しくなる算数塾




中学受験の算数 速さ 攻略のカギは図の使い方にあり 日経xwoman




z会の通信教育中学受験コース 教材見本 算数



無料ダウンロード中学受験 算数 速さ 問題 最高のカラーリングのアイデア



中学受験 流水算は 4つ速さを整理すれば簡単に解ける かるび勉強部屋



速さとグラフの問題 中学受験 田中貴 Com



2人の間の距離のグラフ 芝 H19 大問9




中学受験のための学び方参考書 ここから算数 しっかり基礎力 Amazon Com Books



洗足学園中学校年度第1回算数入試問題 5 速さのグラフ 1 解説解答 プロ家庭教師集団スペースoneの中学受験過去問対策
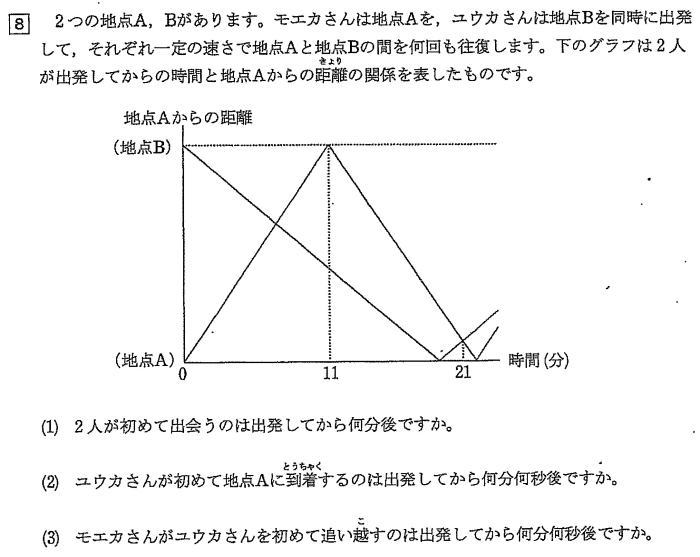



成城中学校年度第3回算数入試問題8 旅人算のグラフ 中学受験から医学部受験までプロにお任せ プロ家庭教師集団スペースone 公式



中学受験算数 和と差の文章題総合 1 01 05 Bw001 算数問題集のアキラストア 通販 Yahoo ショッピング




イメージでわかる中学受験算数問題 旅人算
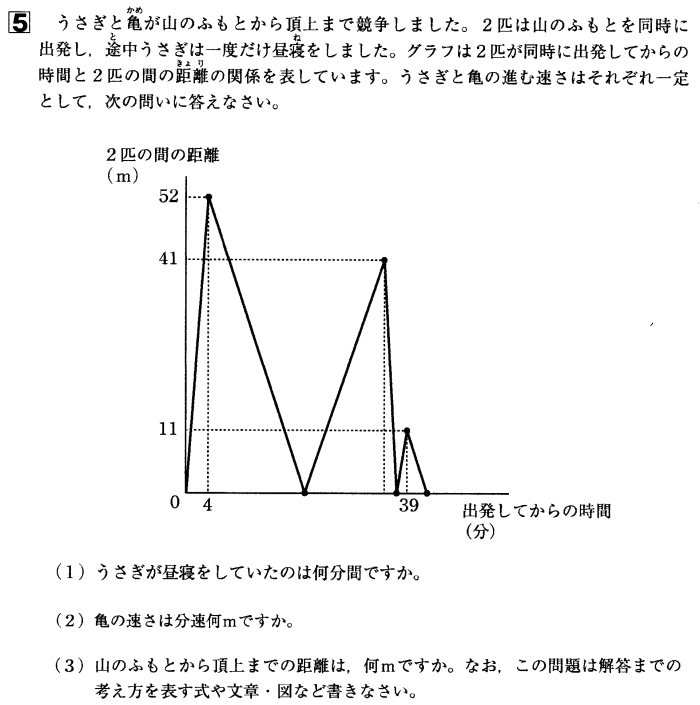



洗足学園中学校年度算数入試問題5 速さのグラフ 中学受験から医学部受験までプロにお任せ プロ家庭教師集団スペースone 公式
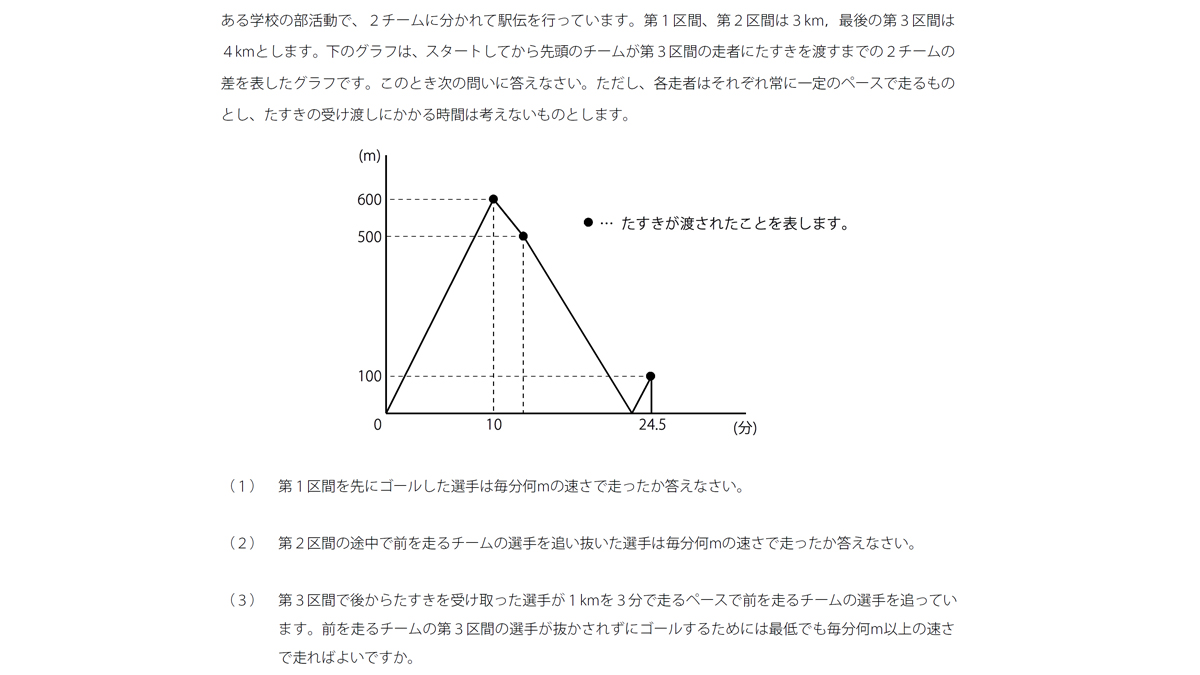



みんなの算数オンライン 最新年 栄東中学校a日程の大問3です グラフの読み取りの速さの問題です 複雑な計算は特にありませんが 意外と難しいかもしれません 解説はこちら T Co Beyh7og4me 中学受験 算数 みんなの 算数オンライン 栄




中学入試 分野別集中レッスン 算数 速さ 中学入試分野別集中レッスン 粟根 秀史 本 通販 Amazon
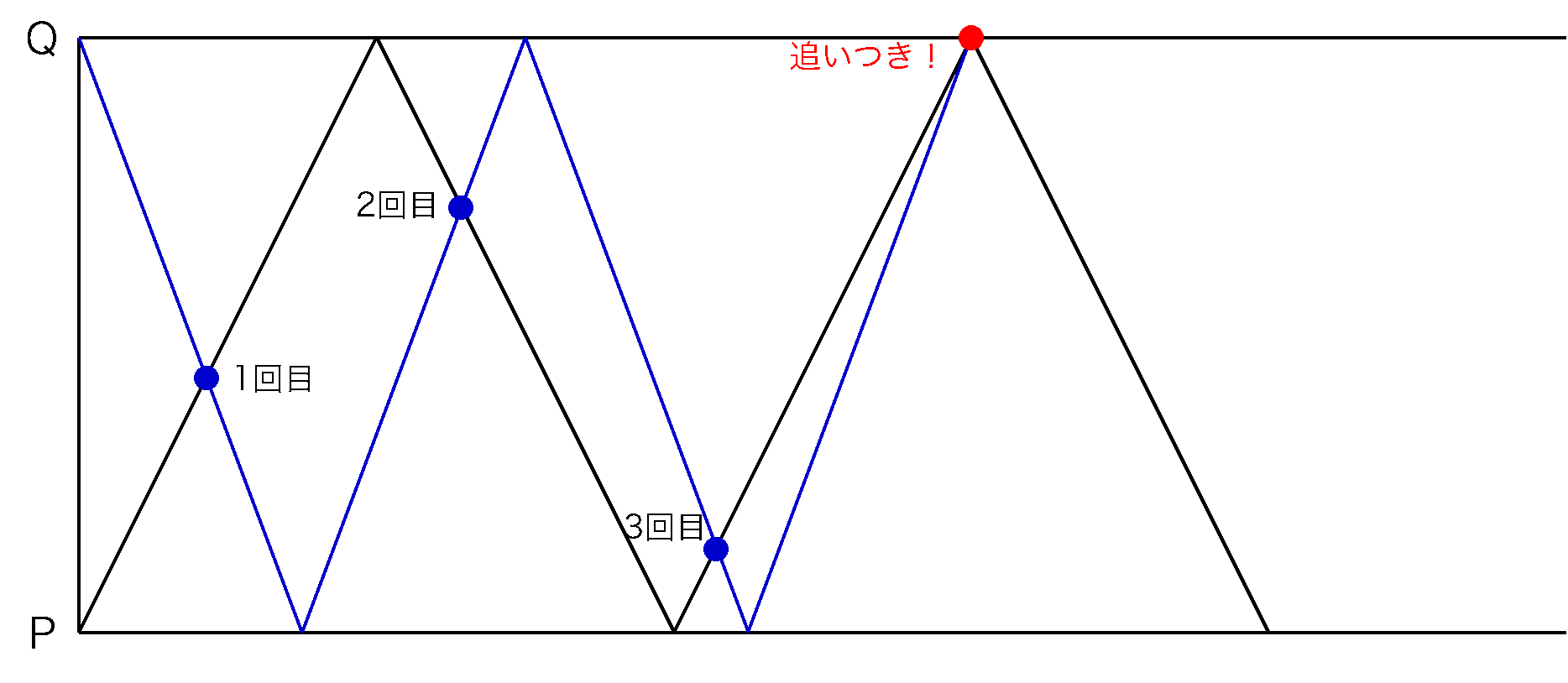



中学受験算数 ダイヤグラムの知られざる 利点 中学受験プロ講師ブログ
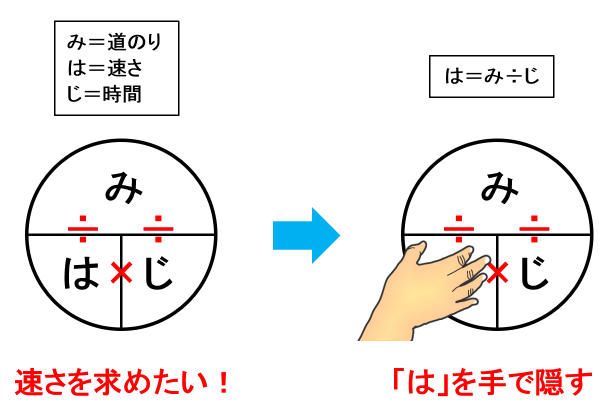



速さ 線分図 面積図 ダイヤグラムがあれば みはじ は要らない みみずく戦略室




中学受験算数 水面の高さと変化のグラフ の授業映像 プリント無料配布 Youtube スタディカフェ




難関中学に合格する グラフで攻略速さのトレーニング ダイヤグラムで 速さ を得意に 算数脳を鍛える 中学受験の通販 井上 慶一 紙の本 Honto本の通販ストア



表とグラフ 中学受験ー算数解き方ポータル
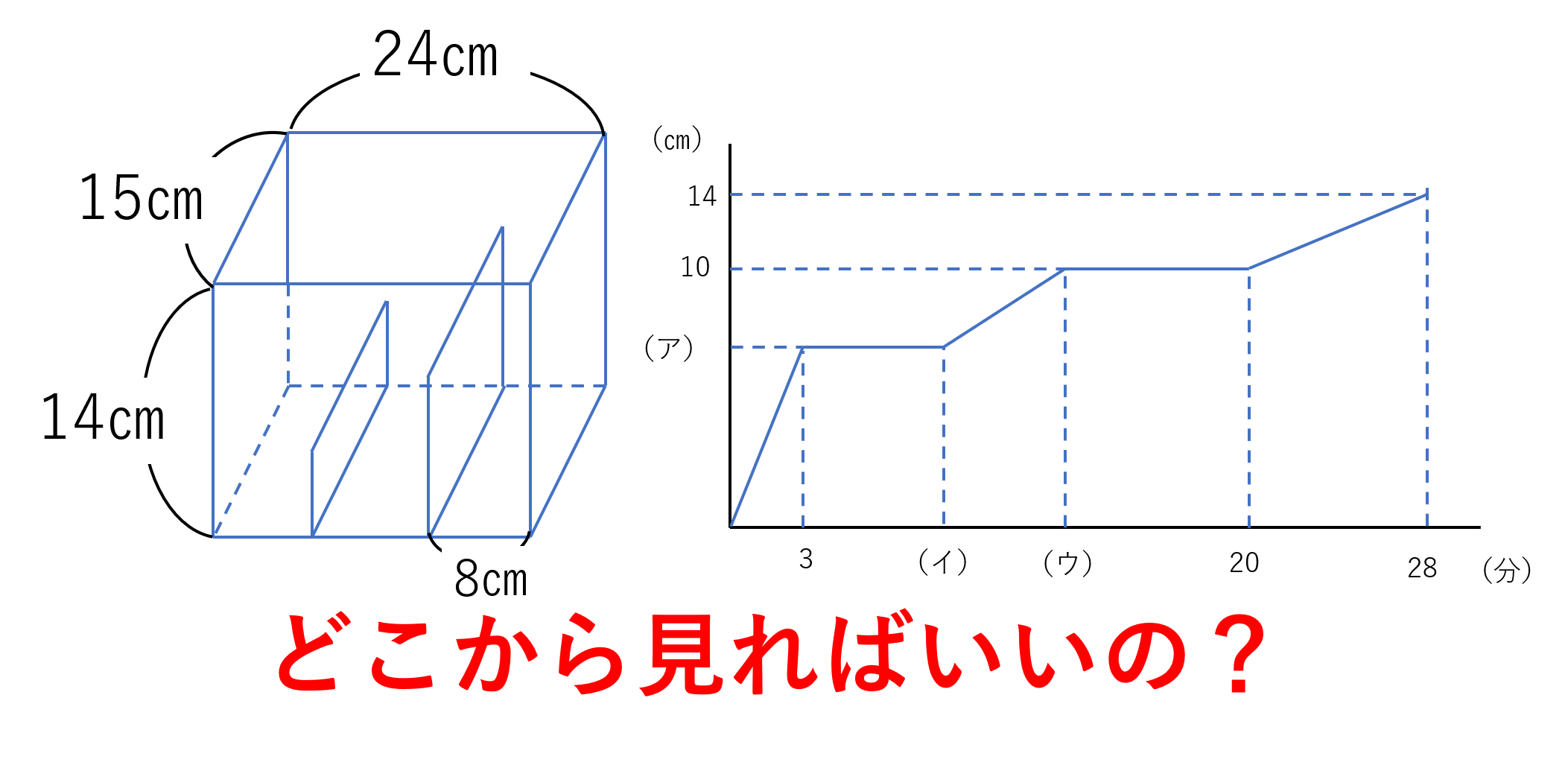



グラフの読み取り方のコツ 算数が得意な子には何が見えているのか 算田数太郎の中学受験ブログ




9月18日5算数授業動画です 中学受験塾act アクト のブログ




中学受験 速さの基本問題を分かりやすく図解 単位 三公式 ダイヤグラム そうちゃ式 受験算数 2号館 図形 速さ



中学受験算数の速さ問題を禁断の技で解いてみる 父ちゃんが教えたるっ




中学受験算数 速さのグラフ ダイヤグラム 小学4年生 6年生対象 毎日配信 Youtube




進行グラフと比
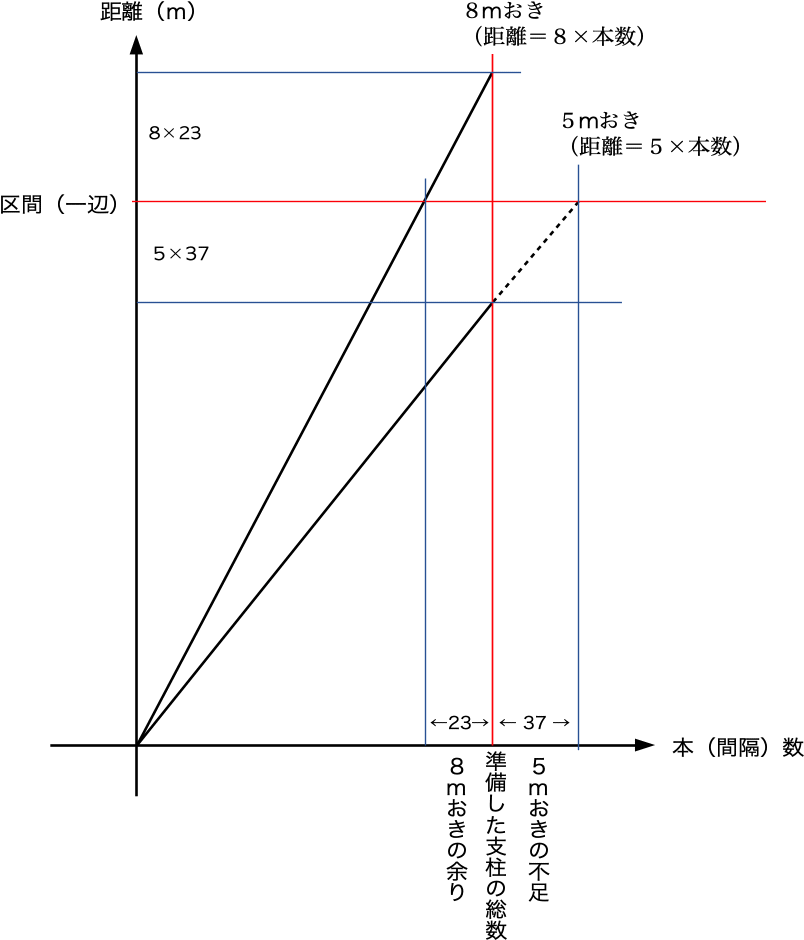



差集め算か比か 受験算数別解集 家庭教師がお手伝い 札幌




算数 速さとダイヤグラム 中学受験 ベネッセ教育情報サイト




中学受験 算数確認チェック26 速さ 速さのグラフ 流水算 グランパは元塾長



A地 B地 中学受験算数 グラフと速さ どう解く 中学受験算数
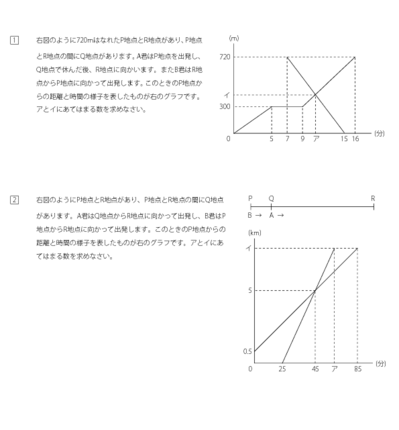



みんなの算数オンライン 中学受験5年 速さ 旅人算 速さとグラフ ダイヤグラム




速さと比 ダイヤグラムで旅人算を図形的に考える 基本編 みみずく戦略室




中学受験算数の全てが分かる 算数の森 ブログ版 速さ
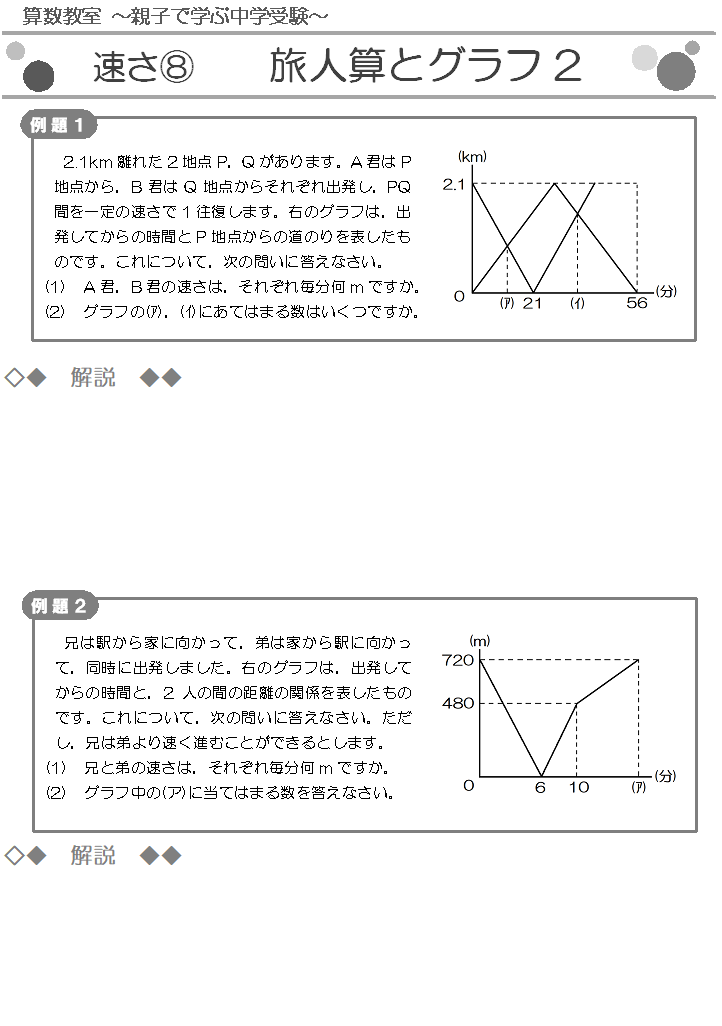



速さ 旅人算とグラフ2 算数教室 親子で学ぶ中学受験




中学受験 算数確認チェック28 速さ 点の移動とグラフ グランパは元塾長


