Thus, the rational number 7/4 lies at a distance of 7 points from 0 towards positive number line (ii) 5/6 on the number line Divide line between two natural number in 6 parts Thus, the rational number 5/6 lies at a distance of 5 points from 0 towards negative number line • Rational Numbers between Two Rational Numbers Between anyLocate √5, √10 and √17 on the number line Solution √5 on the number line 5 can be written as the sum of the square of two natural numbers ie, 5 =1 4 =1 2 2 On the number line, Take OA = 2 units Perpendicular to OA, draw BA = 1 unit Join OB Using Pythagoras theorem, We have, OB= √5 Draw an arc with centre O and radius OBX^2 = 9x 6 9 √105/2, 9 √105/2 What are the solutions to x^2 8x 7 = 0?

Irrational Number Wikipedia
Represent 3/2 on number line
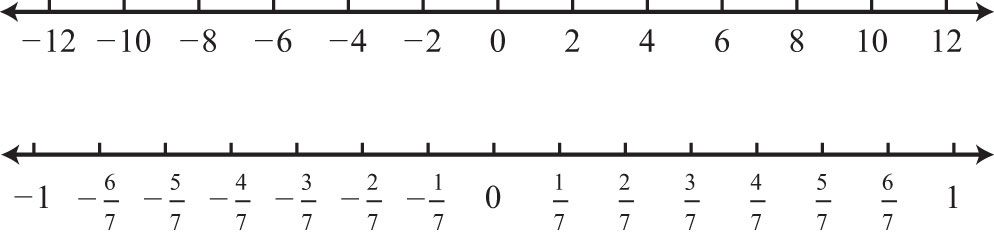
Represent 3/2 on number line- If we express √2 in the decimal form, we observe that it does not terminate and is nonrecurring Such numbers are called irrational numbers The numbers √2 , √3 , √6 , √7 , 2 √3 , 2 – √3 , √2 √3 etc, are examples of irrational numbers All nonterminating and nonrecurring decimal number are irrational numbers If a and b are rational numbers and (√11 − √7)/(√11 √7) = a – b√77, find the value of a and b Finding irrational numbers b/w two numbers;




Find A Point Corresponding To 3 2 On The Number Line
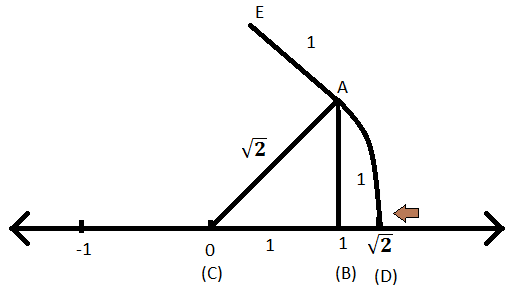
As an example, let us locate √ 2 on the number line This is easy Remember that √ 2 is the length of the diagonal of the square whose side is 1 unit (How?)Simply construct a square and transfer the length of one ofThis can be written as √10 = (√3 2 1 2) The construction steps are shown below Take a line segment AO = 3 units on x axis Here consider 1 unit = 2 cm Draw a perpendicular on O, name it as OC such that OC = 1 unit Now, join AC with √10 Now, take A as centre and AC as radius, draw an arc which cuts the x axis at point ERepresent √32 geometrically on the number line Report Posted by Riya Singh 3 years, 2 months ago CBSE > Class 09 > Mathematics 1 answers Prashant Chaudhary 3 years, 2 months ago
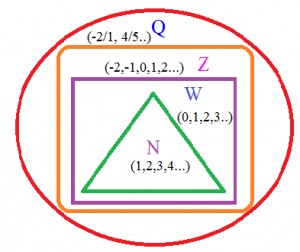
The number √2 is shown on a number line Steps are given to show √3 on the number line using √2 Fill in the boxes properly and complete the activity Activity The point Q on the number line shows the number A line perpendicular to the number line is drawn through the point Q Point R is at unit distance from Q on the line1 Irrational Numbers on the Number Line Where are the points on the number line that correspond to the irrational numbers? Whole numbers Numbers starting from 0 to infinity (without fractions or decimals) ie, Whole numbers= 0,1,2,3 Or, we can say that whole numbers have all the elements of natural numbers and zero Every natural number is a whole number;
5 Join the point O and Point 0 on the number line 6 Measure the joined line of Point 0 and point O 7 Now make an arc from Point O towards the positive side of number line 8 You will get √3 on the number line Now extend √3 by 2 units on the number line 9 Now you have √32 NoteDraw all 90° angle by CompassWe can compare and order real numbers and list them from least to greatest Example 1 Order √22, π 1 and 4 1/2 from least to greatest Then graph them on the number line Solution Step 1 First approximate √22 √22 is between 4 and 5Exercise 15 Question 1 Classify the following numbers as rational or irrational Solution (i) Since, it is a difference of a rational and an irrational number ∴ 2 – √5 is an irrational number (ii) 3 – = 3 – = 3 which is a rational number (iii) Since, = = , which is a rational number



How Do We Represent 3 On Number Line Quora



Solution Where Does 3 2 Go On A Number Line
For example to locate √3 on number line √2 1 (note any √ multiply by the same √ give an integer) 2 1 = 3 3 = √3 Now from this we know we have to take AB = √2cm and BC = 1cm because we have to take AB = √2 we have to first make √2 on number line and then √3 2 1 Finding √2,√3 and√4 on the number line An animated geometric construction 2 a 2 b 2 =c 2 1 2 1 2 =11=2 So Hypotenuse = √2 This line is 1 unit long 3 a 2 b 2 =c 2 ( √2) 2 1 2 =21=3 So Hypotenuse = √3 4 a 2 b 2 =c 2 ( √3) 2 1 2 =31=4 So Hypotenuse = √4 5 Created By Graeme Henchel See more maths stuff at http//henchmaths How to draw root 10 on a number line s Class 9 , Maths , Number Systems Asked by Timothy 2 Answers We can do it by using Pythagoras Theorem We can write √10 = √(9 1) => √10 = √(3 2 1) Construction 1 Take a line segment AO = 3 unit on the xaxis (consider 1 unit = 2cm) 2 Draw a perpendicular on O and draw a line OC = 1



Representation Of Irrational Numbers On The Number Line 2 On Number Line




Represent 2 3 On The Number Line Locate 2 3 On Number Line 2 3 On Number Line Youtube
We need to simplify the numbers in order to classify them √12 = √((4x3)/2) = (2√3)/2 = √3 This is an irrational number An irrational numbers is a type of real number (15)⋅(√3) This number cannot be simplified, but since it is a multiple of an irrational number2 √3 = 2 √3 Rational Number Irrational Number = Irrational Number Eg 7 √3 = 7 √3 Non 0 Rational Number / Irrational Number = Irrational Number 3 / √3 = √3 Q4 The product of any two irrational numbers is A) always an irrational number B) always a rational number C) always an integer D) sometimes rational, sometimes irrational Q5 The decimal expansion of the number √ 2 is A) a finite decimal B) C) nonterminating recurring D) nonterminating nonrecurring Q6 Which of the following is




Draw A Number Line And Locate 2 And 3 On The Number Line Brainly In




Representing Irrational Numbers 2 3 On The Number Line Part 3 Youtube
Step 4 Order the numbers from least to greatest 36, 64, 125, 256 Step 5 Using the order of numbers in step 4, write the given rational and irrational numbers in the order from least to greatest 6 1/3 , 2, √5, 4 2/3 Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here=> √10 = √(3 2 1) Construction 1 Take a line segment AO = 3 unit on the xaxis (consider 1 unit = 2cm) 2 Draw a perpendicular on O and draw a line OC = 1 unit 3 Now join AC with √10 4 Take A as center and AC as radius, draw an arc which cuts the xaxis at point E 5 The line segment AC represents √10 unitsRepresent root √32 on the number line, Locate (root 3)2 on number line, √32 on number line,1) Represent √2 (root 2) on number linehttps//youtube/tbulE99




How To Represent Root 2 On Number Line With Steps Brainly In




2 Root 3 On Number Line How To Represent 2 Root 3 On Number Line 2 3 On Number Line Youtube
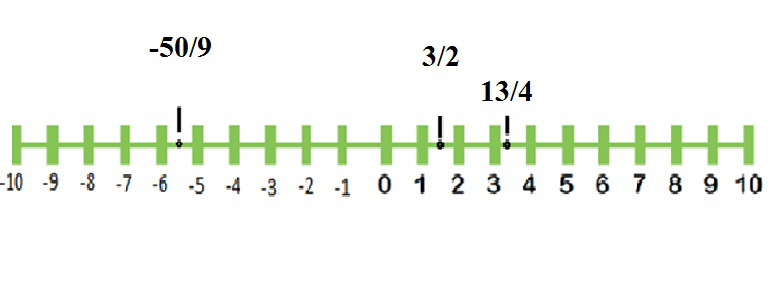
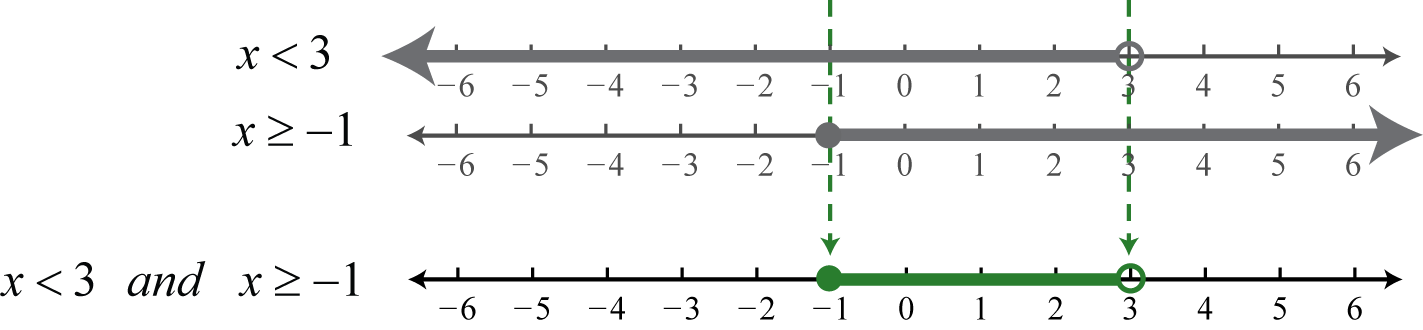
108 Chapter 3 Quadratic Equations and Complex Numbers 32 Exercises Dynamic Solutions available at BigIdeasMathcom In Exercises 5–12, fi nd the square root of the number (See Example 1) 5 √ — −36 6 √ — −64 7 — — — — — — 2 3 6 2Write 5 rational numbers between 5 & 6 7 Write 4 irrational numbers between √ & √ 8 Show that 1 ⃐ can be in the form (rational number) 9 √Is an irrational number Give reason 10 Represent on a number line √(a) 2 √(b) √5 (c) 10 11 Represent 4735 using successive magnification 12Also solve by showing graph overlaid on number line Make 0 on right side Factor by grouping Critical numbers zeros 4/3, 2, 2 no undefined Test points 3 (F), 0(T), 3/2(F), 3 (T) Answer (−2, 4/3) U (2, ∞) Also solve by showing graph overlaid on number line




How Do We Represent 2 3 On A Number Line Quora



Real Numbers Geeksforgeeks
Q5 Divide 10√ by 5√ Q6 Write whether the rational numberFirstly some examples of the square root of a squared number √2 2 = √4 = 2 √5 2 = √25 = 5 Looking at these two examples, it could be reasonable to assume that it's always the case that √a 2 = a But this is not quite the case For example with 3 3 × 3 = 9 Thus √ 3 2 = √9 = 3The distance formula is derived from the Pythagorean theorem The given distance between two points calculator is used to find the exact length between two points (x1, y1) and (x2, y2) in a 2d geographical coordinate system Draw a rightangled triangle with the line formed by the points, the distance between the two points can be calculated by finding the horizontal (x 2 x 1) and



Represent Root 3 On Number Line Youtube




Q3 Represent The Following Num Lido
Distance on a Number Line Distance in the Coordinate Plane AB x 1 x 2 AB = x 1 x 2 or x 2 x 1 Distance Formula y 0 x B(x 2, y2) A(x 1, y1) d = 2√ """""(x 9 2 x 1) (y 2 y 1)2 Use the number line to find AB AB = (4) 2 = 6 = 0123 AB Find the distance between A(2, 1) and B(1, 3) Distance Formula d = √Real numbers on a number line; As we know irrational number divided by a rational number results in an irrational number Question 4 Represent \(\sqrt{93}\) on the number line Solution To represent \(\sqrt{93}\) on the number line We mark a point B on the number line so that AB = 93 units Again mark a point C so that BC = 1 unit



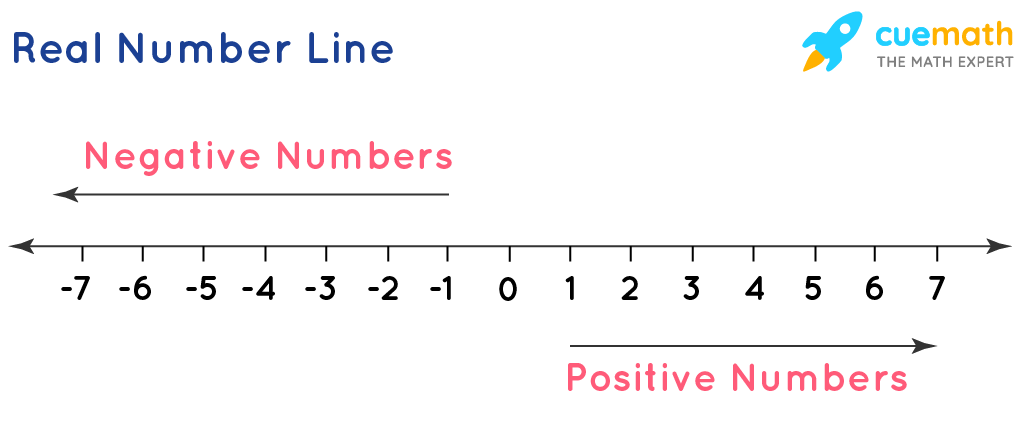
Real Numbers And The Number Line



Fractions As Numbers On A Number Line Grade 3 Mathematics
Jul 11,21 represent √32 on number line EduRev Class 9 Question is disucussed on EduRev Study Group by 556 Class 9 StudentsWhich are the solutions of the quadratic equation?However, every whole number is not a natural number (ii) Every integer is a whole number Solution False




Represent The Following Rational Numbers On The Number Line 5 2 3 4 1 6 11 6 11 3 Brainly In
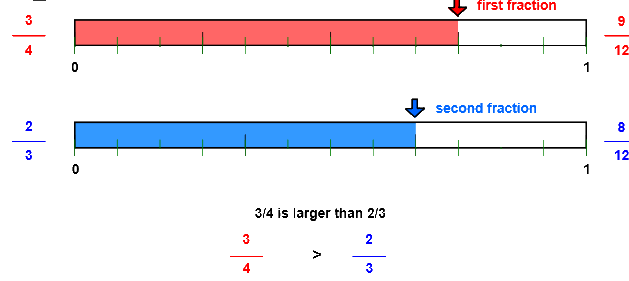



Compare Fractions With Number Line Models
When written with a rational denominator, the expression 2√3/3√2 can be simplified as (1) √2/3 (2) √3/2 (3) √6/3 (4) 2/3 the number line The point at which number line get intersected by arc is at √5 distance from 0 because it is a radius of the circle whose center was A Thus, √5 is represented on the number line as shown in the figureRationalise the denominator of 1/√3√2 and hence evaluate by taking √2 = 1414 and √3 = 1732,up to three places of decimal




Represent 2 Root 3 On A Number Line Maths Number Systems Meritnation Com
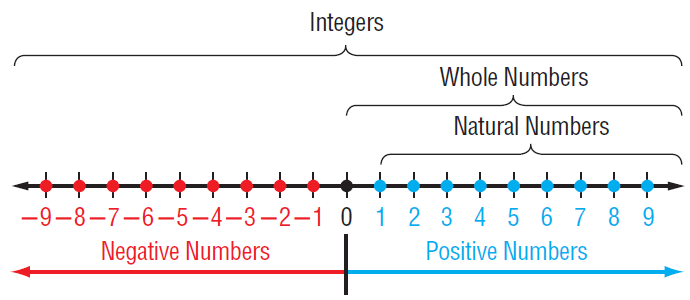



Rational Numbers On The Number Line
Number System – Exercise 11 A number 's' is called irrational, if it cannot be written in the form p / q, where p and q are integers and q ≠ 0 Some examples are √2 , √3, √15, π, Remark Recall that when we use the symbol √, we assume that it is the positive square root of the number Example18 Rationalize the denominator of 1/(2√3) To rationalize, We multiply and divide by 2 root 3 Let's check the video 1/(2√3) = 1/(2√3) × (2 −√3So now you have √(3) length You have to represent 2√(3) in number line So first mark 2 in number line and then from 2 use geometric compass and make a circle with the same length of √(3) as radious in number line So between 1 and 2 where the circle cuts that is 2√(3) and between 2 and 3 where t




Integer Number Line Video Lessons Examples And Solutions
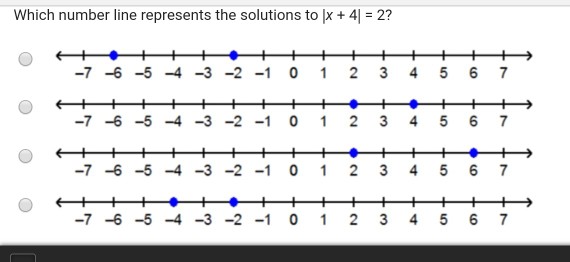



Which Number Line Represents The Solutions To X 4 Chegg Com
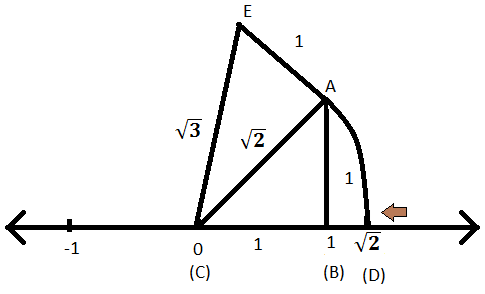
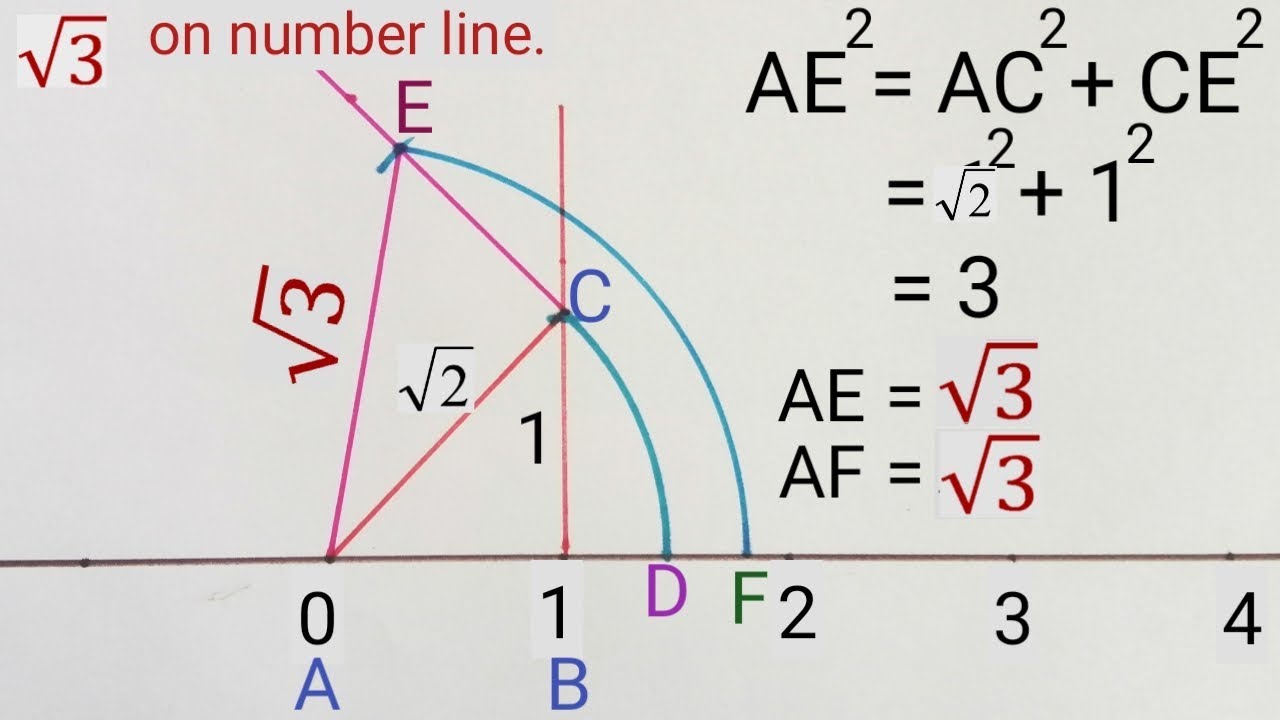
X = 7 and x = 1 The area of a rectangular room is 750 square feet The width of the room is 5 feet less than the length of the room Which equations can be used to solve for y, the length of the room?9 Order √ _ 3 , 2 π, and 15 from least to greatest Then graph them on the number line (Example 2) √ _ 3 is between and , so √ _ 3 ≈ π ≈ 314, so 2π ≈ From least to greatest, the numbers are , , 10 Four people have found the perimeter of a forest using different methods Their results are given An irrational number √2 is represented on the number line Learning Outcome Students can represent any irrational number on number line by using above method eg, (√3) 2 = (√2) 2 (1) 2 At M, by paper folding draw perpendicular BM on the number line of 1 unit Join OB With O as centre and OB as radius draw an arc intersecting the line




How Do We Represent 2 3 On A Number Line Quora




Locate 2 On Number Line Maths Questions
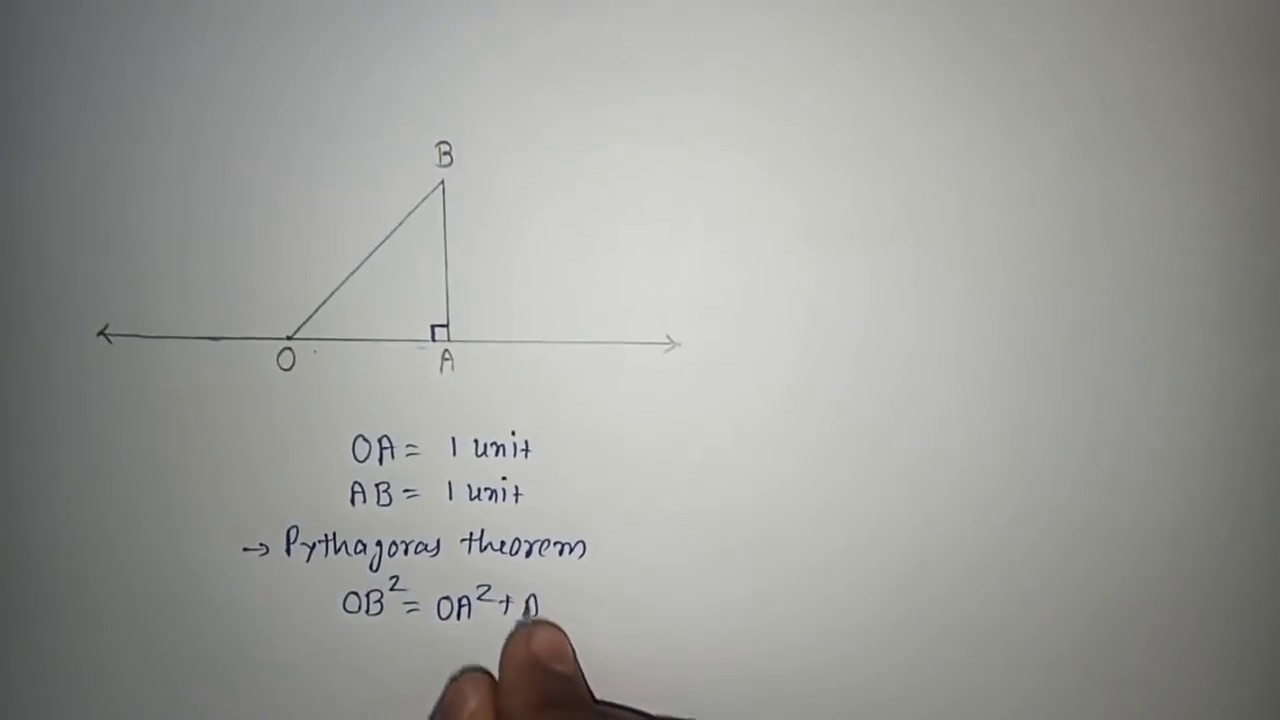
About the Author Davneet Singh Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 10 years Represent √3 on the number line Solution On the number line, take OA = 1 unit Draw AB = 1 unit perpendicular to OA Join OB Again, on OB, draw BC = 1 unit perpendicular to OB Join OC By Pythagoras Theorem, we obtain OC = √3 Using compasses, with centre O and radius OC, draw an arc, which intersects the number line at point DThen, extend a line from 0 to the point you just plotted That line is the visual representation of the number 32i Some other properties are represented by the line on the Argand diagram The length of the line represents the modulus of the number √(3 2 2 2) = √13 The line also forms an angle with the positive side of the real axis
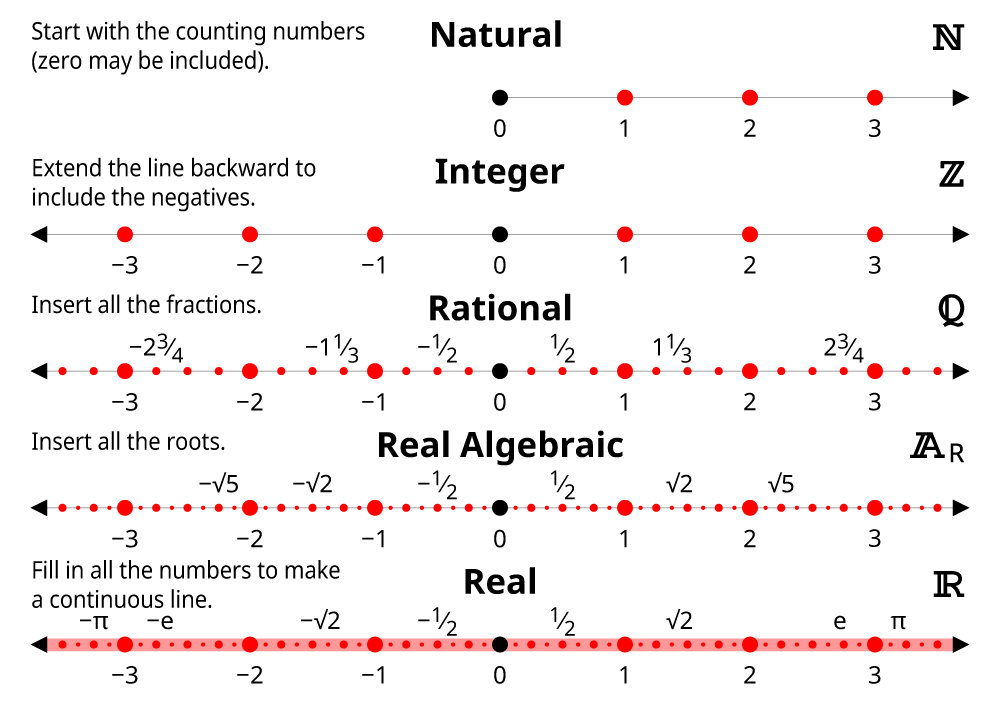



Number Sets




Represent 2 Root 5 On The Number Line Youtube
answer answered 2 Locate √3 on the number line 3 Locate √10 on the number line 4 Locate √18 on the number line please jaldi batao koi detail maTake O as centre and OB 3 as radius, draw an arc which cuts the number line at D Point D represents √5 on the number line Ex 12 Class 9 Maths Question 4 Take a large sheet of paper and construct the 'square root spiral' in the following fashion Start with a point O and draw a line segment OP 1, of unit lengths Draw a line segment P 1Pets & Animals Represent root 23 on the number line, Locate root 23 on number line, √23 on the number line, 1) Represent √2 (root 2) on number line https//youtube/tbulE993EfM 2) Represent √3 (root 3) on the number line https//youtube/SuKSbqkYRbk 3) Represent √5 (root 5) on the number line



Solution How Do I Graph The Fraction 10 7 On A Number Line
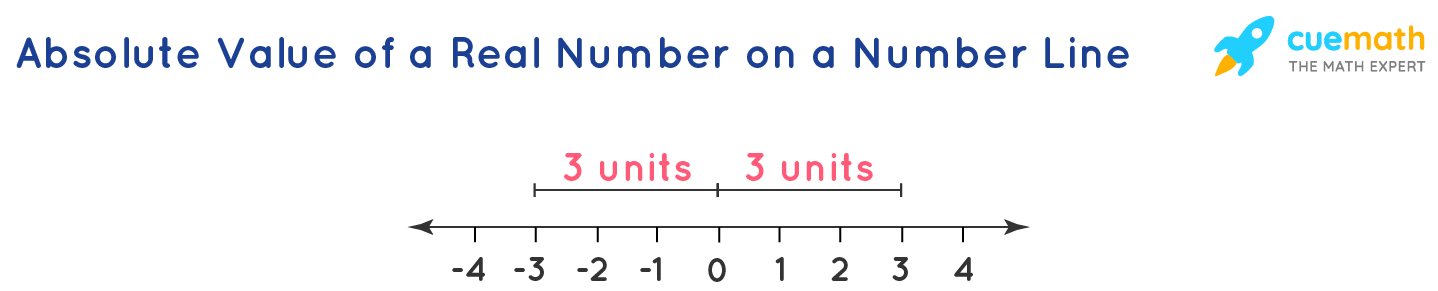



Representation Of Real Numbers On Number Line Steps Method Real Number Line Examples
=> √12 = √{32 (√3)2 } So, for representing √12 on number line, first we have to represent √3 on number line Now, √3 = √(2 1) => √3 = √{(√2)2 12 } 2 Every real number can be represented at a point on number line or real number lineIdentify a rational number among the following numbers 2 √2, 2√2, 0 and π Q2 Find the value of √(3)2 Q3 Find two irrational numbers between 2 and 25 Q4 How many rational numbers can be found between two distinct rational numbers?




Locate 3 On Number Line Maths Questions




What Is A Real Number In Math Solved




Locate 2 On Number Line Maths Questions



Eg4 Nic In Jnv Dfiles Ebooks Ir Numbersystem Pdf



Representation Of Real Numbers On Number Line Steps Method Real Number Line Examples



Q Tbn And9gcqyelewoszlg O1ndidwzu1b7g0lcrdagbpxs0nttrx5cedumj5 Usqp Cau




Find A Point Corresponding To 3 2 On The Number Line




Represent 2 2 On The Number Line Youtube



3 Consider The Expressions Square Root Of 15 S Gauthmath




Real Numbers And The Number Line




Which Number Line Best Shows The Position Of Square Root 13 Brainly Com




Integer Number Line Video Lessons Examples And Solutions




Irrational Number Wikipedia



Representation Of Real Numbers On Number Line Steps Method Real Number Line Examples




How To Locate Root 3 On A Number Line Spiral Method Mathematics Topperlearning Com Y0wmee




Represent 9 3 On The Number Line



Representation Of Irrational Numbers On The Number Line 2 On Number Line
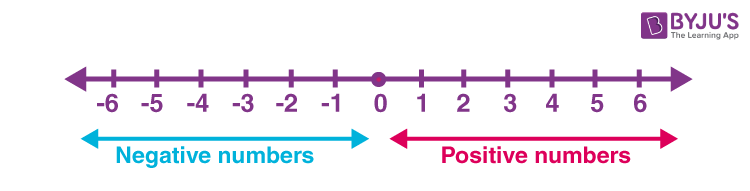



Number Lines Definition Representation 1 To 100 Examples
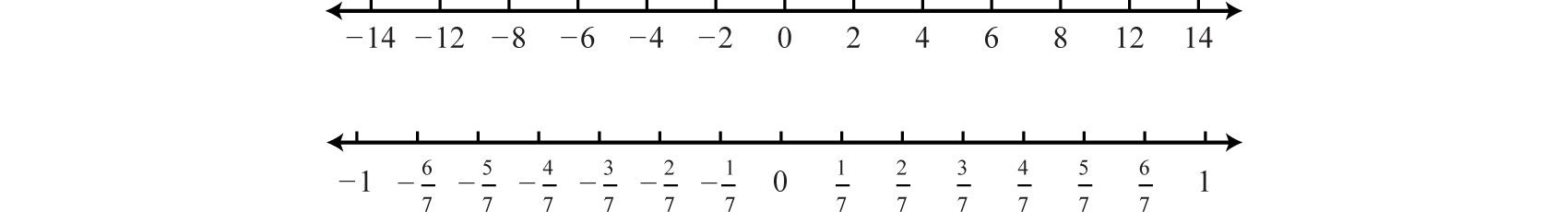



1 1 Real Numbers And The Number Line Mathematics Libretexts



How Do We Represent 3 On Number Line Quora




Solve The Inequality Other Than O Graph The Chegg Com
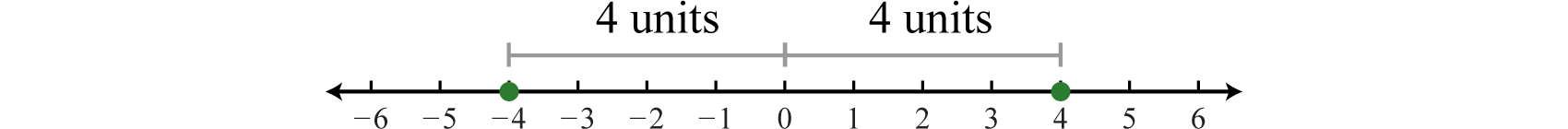



1 1 Real Numbers And The Number Line Mathematics Libretexts



Q Tbn And9gcqyelewoszlg O1ndidwzu1b7g0lcrdagbpxs0nttrx5cedumj5 Usqp Cau




Represent The Following Numbers On The Number Line 7 7 2 3 2 And 12 5 Youtube




The Number Line Key Stage 2
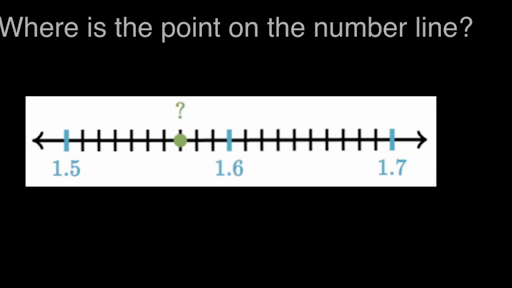



Identifying Hundredths On A Number Line Video Khan Academy



Representation Of Rational Numbers On A Number Line Steps Examples



Divide Fractions With Number Line Models




Graph The Number Below On A Number Line Squareroot Chegg Com



How Do We Represent 2 3 On A Number Line Quora




Represent 2 Root 3 On Number Line Mathematics Topperlearning Com R3keaipp




Transforming The Square Root Function Video Khan Academy




Represent The Given Rational Numbers On The Same Number Line A 2 3 And 4 5 B 3 2 And 5 3 Please Brainly In




Real Numbers Geeksforgeeks




Represent 3 On Number Line Brainly In




Absolute Value And Number Lines Video Khan Academy



Locate Root 3 On The Number Line Represent Root 3 On Number Line Root 3 On Number Line Youtube




Represent 2 Root 3 On Number Line Mathematics Topperlearning Com R3keaipp




Represent Root 2 3 5 10 13 On Number Line Chapter 1 Class 9 Maths Part 2 Step By Step Youtube



How Do We Represent 2 3 On A Number Line Quora



Review Of Real Numbers And Absolute Value



Finding Domains Using Number Lines Math Central
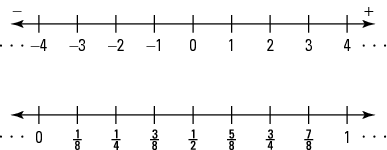



Graphing On A Number Line



The Number 2 Is Shown On A Number Line Steps Are Given To Show 3 On The Number Line Using 2 Sarthaks Econnect Largest Online Education Community
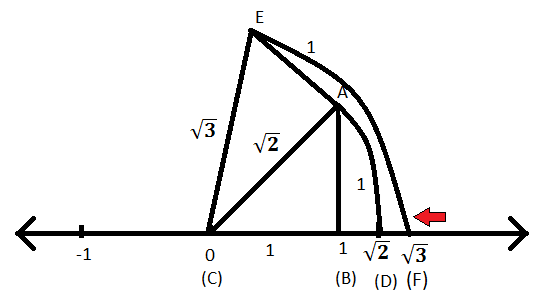



Representation Of Irrational Numbers On The Number Line 2 On Number Line



Square Root Of 2 Wikipedia




Represent 2 Upon 3 On The Number Line Brainly In
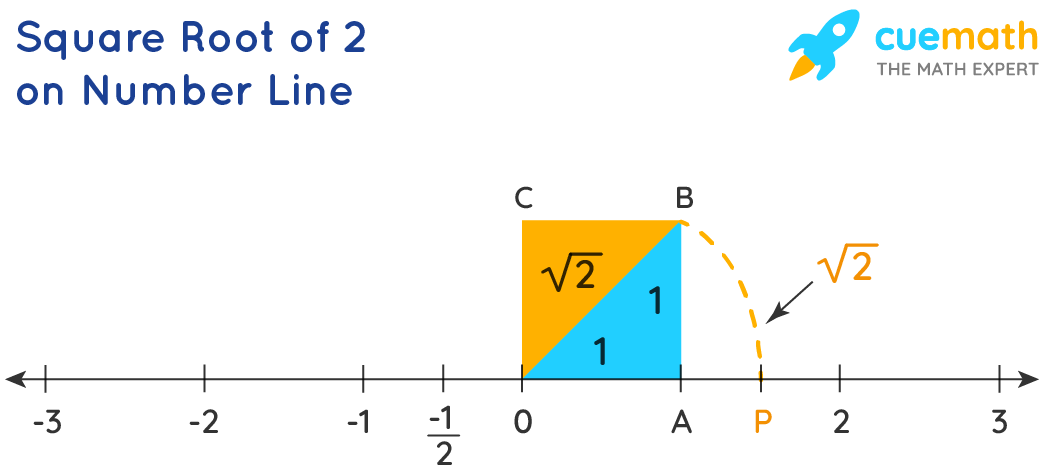



Square Root Of 2 How To Find The Square Root Of 2 Cuemath
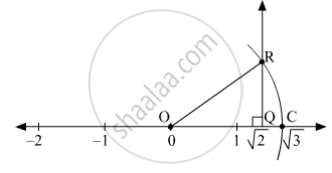



The Number 2 Is Shown On A Number Line Steps Are Given To Show 3 On The Number Line Using 2 Fill In The Boxes Properly And Complete The Activity Mathematics Shaalaa Com



Number Lines Definition Representation 1 To 100 Examples




The Number Line Key Stage 2




Locating And Ordering Decimals With A Number Line Prealgebra



Represent The Following Numbers On The Number Line 7 7 2 3 2 And 12 5 Sarthaks Econnect Largest Online Education Community




Ask Questions For Cbse Class 9 Maths Number Systems



Square Root Of 3 Wikipedia
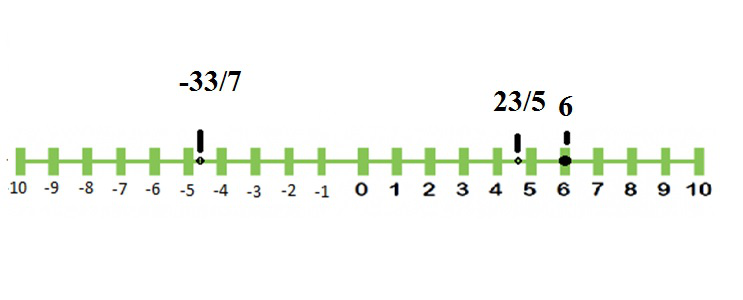



Real Numbers Geeksforgeeks



How Can We Represent Root 2 On The Number Line Quora
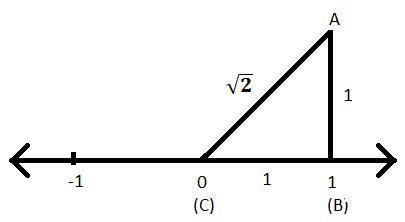



Representation Of Irrational Numbers On The Number Line 2 On Number Line
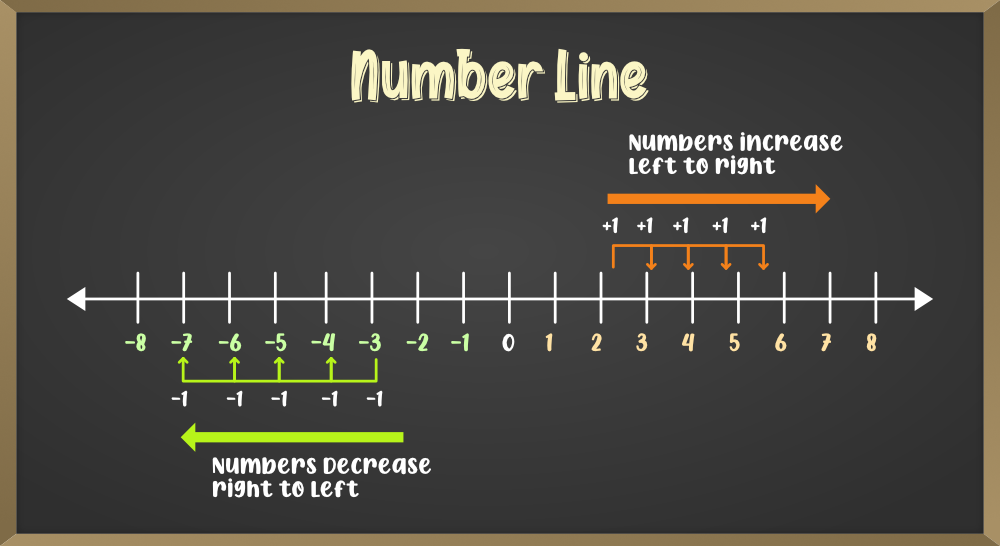



Number System In Maths Geeksforgeeks



Q Tbn And9gcq3dci71zygo5srkpm 1gchk9gizckeiw8n16f8dr 6i3fs936 Usqp Cau



Represent Square Root Of 7 5 On The Number Lin Gauthmath




Graphing Rational Numbers On A Number Line Video Lesson Transcript Study Com
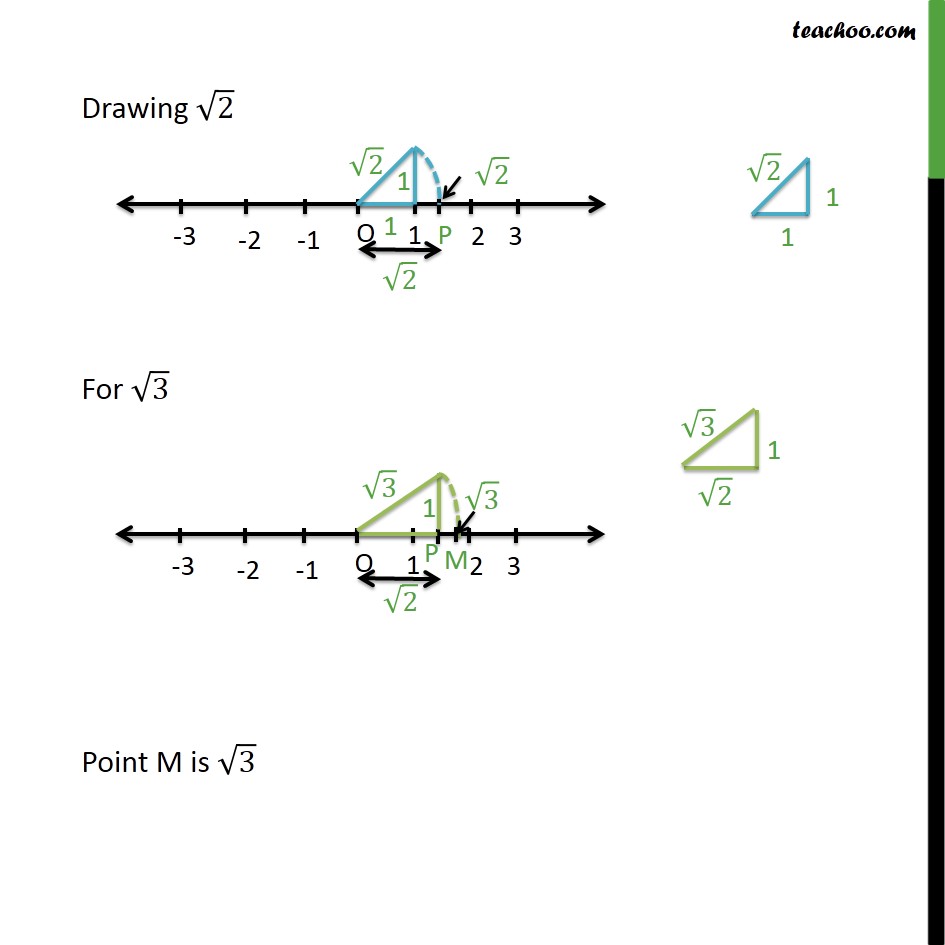



Represent Root 3 On The Number Line With Video Chapter 1 Class 9



Represent The Following Irrational Numbers On The Number Line I 3 Ii 4 7 Iii 6 5 Sarthaks Econnect Largest Online Education Community




Represent Root 2 On The Number Line With Video Teachoo




How To Draw 3 Root 2 On Number Line Mathematics Topperlearning Com G09h7see




Represent Root 3 On The Number Line With Video Chapter 1 Class 9




Represent Root 3 On The Number Line With Video Chapter 1 Class 9




Graphing Rational Numbers On A Number Line Video Lesson Transcript Study Com
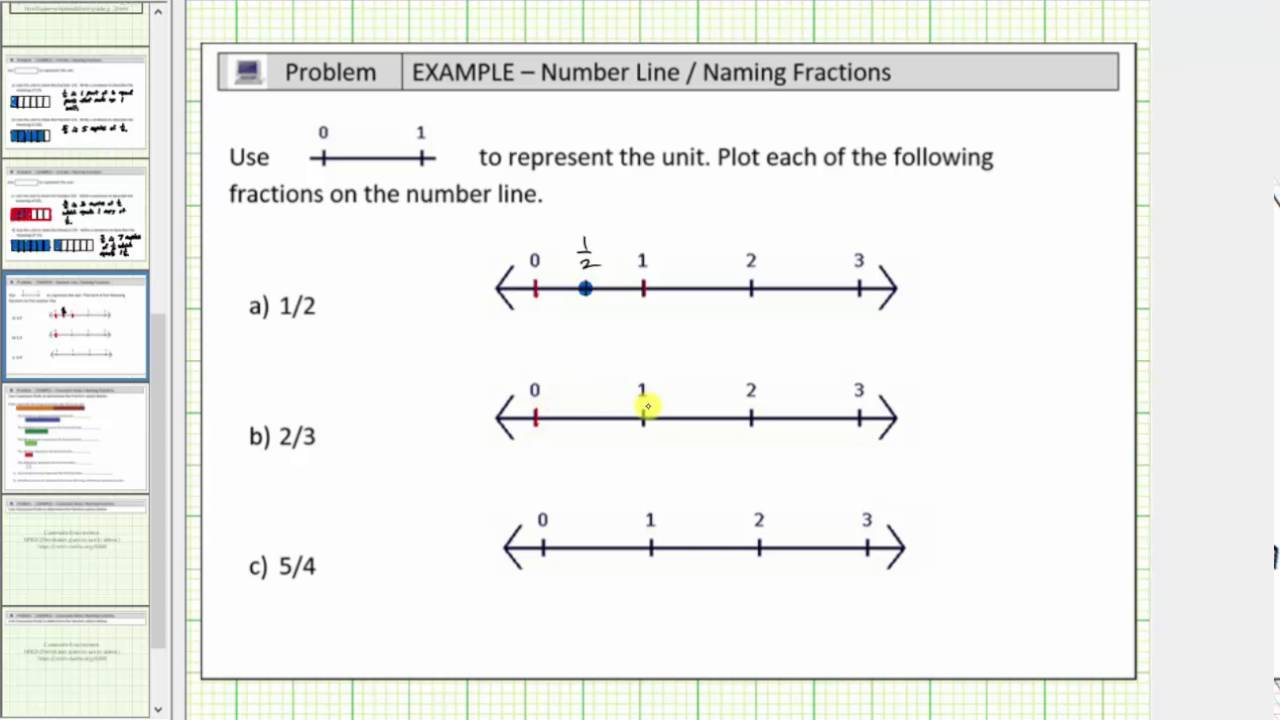



Plot Fractions On The Number Line Youtube




How Can We Represent 2 On A Number Line Quora
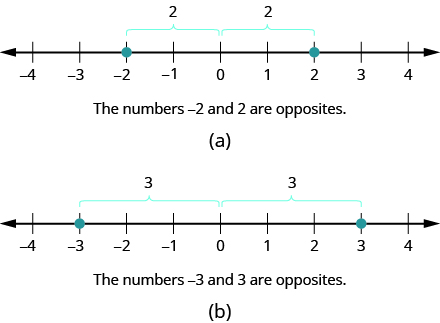



Notation And Definition Of The Set Of Integers Mathematics For The Liberal Arts Corequisite
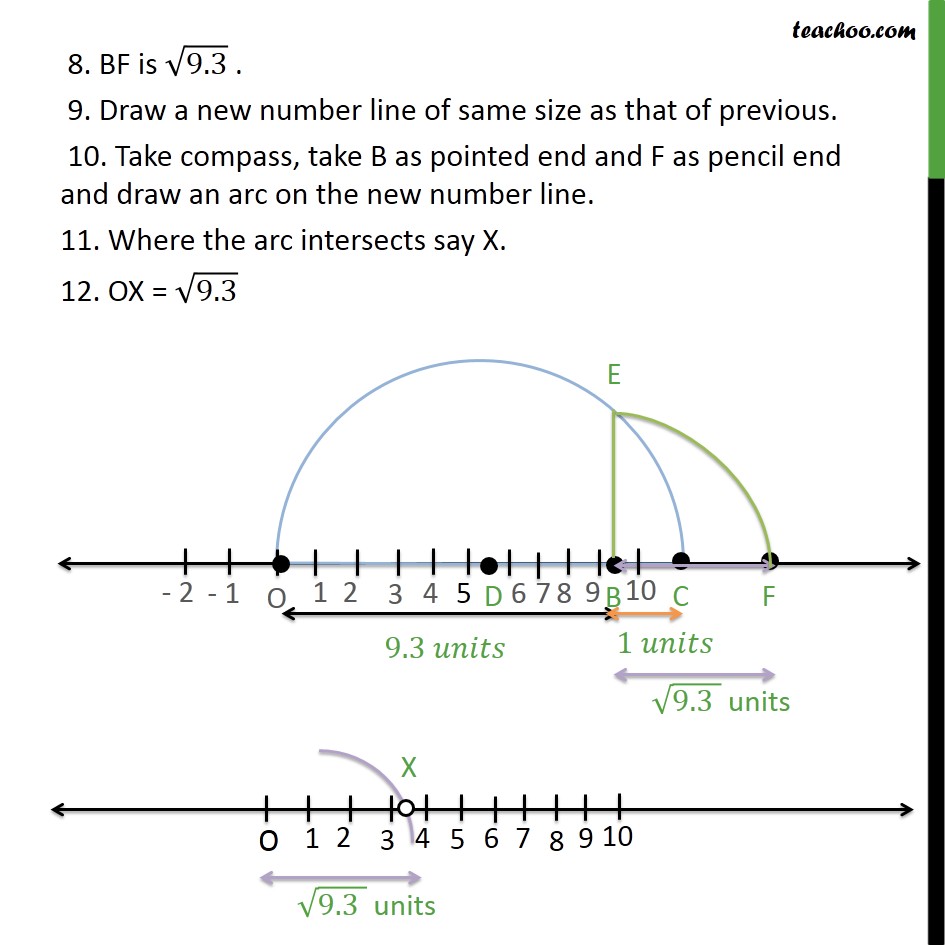



Ex 1 5 4 Ex 1 5




Q3 Represent The Following Num Lido



Number Lines Definition Representation 1 To 100 Examples



1




Represent The Real Number Root 2 Root 3 Root 5 On A Single Number Line Brainly In




For A Complex Number 1 2 J Square Root 3 2 Find Chegg Com


